仕事算-2-3（白百合学園中学2022/サッカー部員がグラウンド整備する仕事）

1 問題
2 解答

問題

問題（白百合学園中学2022/サッカー部員がグラウンド整備する仕事）

ある学校のサッカ一部員が、2つのグラウンドA、Bの整備をしました。AはBの3倍の広さです。はじめに全員でAを1時間整備しました。その後、部員の人数を半分ずつに分けて、一方がA、もう一方がBの整備をしました。15分後にAの整備が先に終わったところでその日の作業を終え、Bの残りの整備を次の日にすることにしました。2日目は部員の何人かでBの残りの整備をしたところ、42分かかりました。ただし、グラウンド整備をする1人あたりの仕事量は同じであるとします。

（1） A全体の広さは、はじめの1時間で整備した部分の広さの何倍にあたりますか。
（2）もし2日目に全員でBの残りの整備をしたとすると、何分かかりますか。
（3）実際に、2日目にBの残りの整備をした部員の人数は何人ですか。ただし、サッカ一部員の人数は50人以上60人以下です。

Amazonブランドのタブレット［Fire HD 10 Plus タブレット10.1インチ］フルHDディスプレイ(1920×1200)だから広くて見やすく家勉の必需品。

解答

解答を開く

（1）
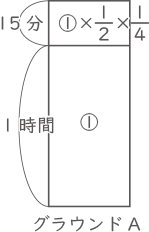
はじめの1時間の仕事量を①とすると、次の15分は$ \displaystyle \frac{1}{2} $の人数で$ \displaystyle \frac{1}{4} $の時間がかかったので仕事量は①×$ \displaystyle \frac{1}{2} $×$ \displaystyle \frac{1}{4} $。
仕事量と広さは比例するので、
（はじめの1時間で整備した部分の広さ）：（次の15分で整備した部分の広さ）＝①：（①×$ \displaystyle \frac{1}{2} $×$ \displaystyle \frac{1}{4} $）＝8：1。
よって、
（A全体の広さ）：（はじめの1時間で整備した部分の広さ）
＝9：8
$ \displaystyle \frac{9}{8} $＝1$ \displaystyle \frac{1}{8} $倍。

（答え）　1$ \displaystyle \frac{1}{8} $倍

（2）
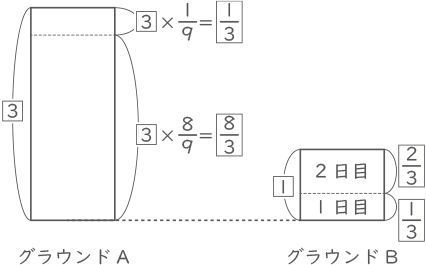
グラウンドA，Bの面積比は$ \fbox{3} $：$ \fbox{1} $なので、
問1からグラウンドAの1時間で整備した面積は$ \fbox{3} $×$ \displaystyle \frac{8}{9} $＝$ \fbox{ $ \displaystyle \frac{8}{9} $ } $。
また、15分で整備した面積は3×$ \displaystyle \frac{1}{9} $＝$ \fbox{ $ \displaystyle \frac{1}{3} $ } $で、これはグラウンドBの1日目に整備した面積と同じ。よって、グラウンドBの2日目に整備した面積は$ \fbox{ $ \displaystyle \frac{2}{3} $ } $。
倍の面積を倍の人数で整備したので、かかる時間は同じ15分。