問題
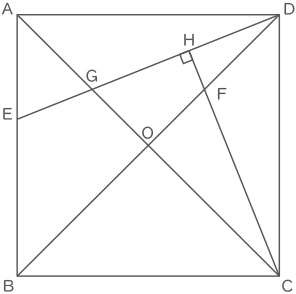図のような，対角線AC，BDの長さが14cmの正方形ABCDにおいて，対角線の交わる点をOとします。またAE：EB＝2：3，角CHE＝90゜です。
（1） 三角形DGOの面積は□cm2です。
（2） OFの長さは□cmです。
教室には遠くて通えない、通塾負担を減らしたい。もしくは他の習い事が忙しくて、通塾の時間が取れない・・・ そんなご家庭に最適！ 4大塾に通いながら弱点補強を家庭教師に任せているご家庭も多々、塾のクラスを上げるためにピンポイントでうまく利用しましょう。なにはともあれ資料請求してお子さんに合うか見てみましょう。
解答
- 解答を開く
-
図のような，対角線AC，BDの長さが14cmの正方形ABCDにおいて，対角線の交わる点をOとします。またAE：EB＝2：3，角CHE＝90゜です。（1） 三角形DGOの面積は□cm2です。
（2） OFの長さは□cmです。（1）
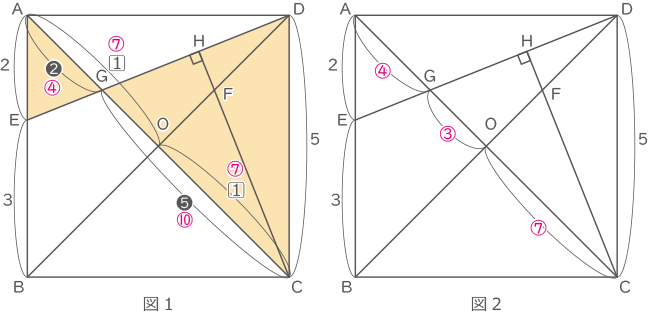
図1のように相似な三角形より
AO：OC＝$ \fbox{1} $：$ \fbox{1} $
AG：GC＝❷：❺
連比として考え、2×7＝14から比をふりなおすと、図２のようにAG：GO：OC＝④：③：⑦となる。三角形DGOの面積＝三角形OADの面積×$ \displaystyle \frac{③}{⑦} $＝$ \displaystyle \frac{49}{2} $×$ \displaystyle \frac{3}{7} $＝10.5cm2
（答え） 10.5
（2）
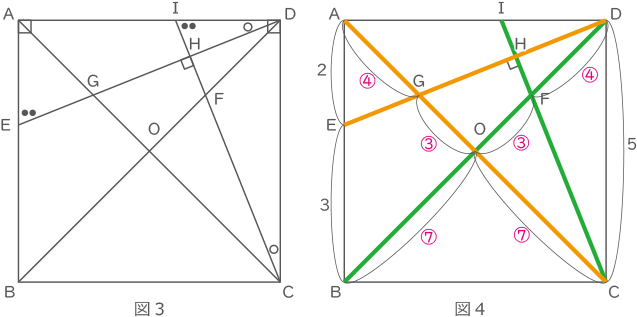
図３のように直線CHを延長し、交点Iをつくる。
三角形AEDと三角形DICは合同とわかる。
図４のように線を色分けするとOF：FD＝③：④が見えてくる。
OFの長さ＝7×$ \displaystyle \frac{③}{⑦} $＝3cm
（答え） 3
合同な三角形が見つかれば、あっという間に解けるが、見つからなければ答えは出てこない。
兎に角、手を動かして色々と補助線を引いてみよう。眺めているだけでは時間だけが経つばかり。
