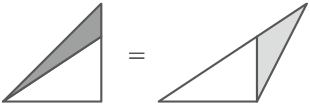問題
問題(共通する面を利用して面積を求める)
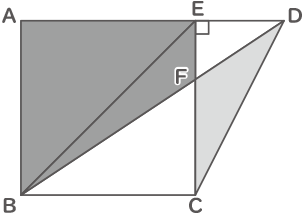
下の図は、正方形と、正方形の辺と同じ長さの辺を持つ直角三角形をピッタリと合わせ、その中に直線を引いたものです。四角形ABFEの面積が216cm2、三角形CDFの面積が54cm2のとき、台形ABCDの面積を求めなさい。
塾、そして弱点補強にプロ家庭教師の「中学受験家庭教師ドクター」
4.12
教室には遠くて通えない、通塾負担を減らしたい。もしくは他の習い事が忙しくて、通塾の時間が取れない・・・ そんなご家庭に最適! 4大塾に通いながら弱点補強を家庭教師に任せているご家庭も多々、塾のクラスを上げるためにピンポイントでうまく利用しましょう。なにはともあれ資料請求してお子さんに合うか見てみましょう。
解答
- 解答を開く
-
下の図は、正方形と、正方形の辺と同じ長さの辺を持つ直角三角形をピッタリと合わせ、その中に直線を引いたものです。四角形ABFEの面積が216cm2、三角形CDFの面積が54cm2のとき、台形ABCDの面積を求めなさい。



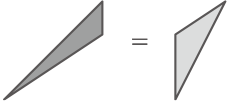
BEに線を引くと、底辺と高さが同じ2つの三角形は同じ面積とわかる。

よって、共通部分を取り除いた2つの三角形も同じ面積54cm2。
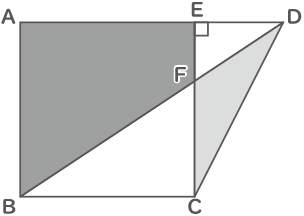
三角形ABEの面積が216-54=162cm2となるので、正方形の面積は324cm2、1辺は18cmとなる。
三角形BFEが54cm2とわかったので、EF=54×2÷18=6cm、CF=18-6=12cm。
三角形FBCと三角形FDEは相似な三角形なので、EF(①):CF(②)=DE:BC(18)からDE=9cm。
よって、台形ABCDの面積=(18+9+18)×18÷2=405cm2。(答え) 405cm2
ではまた~