問題
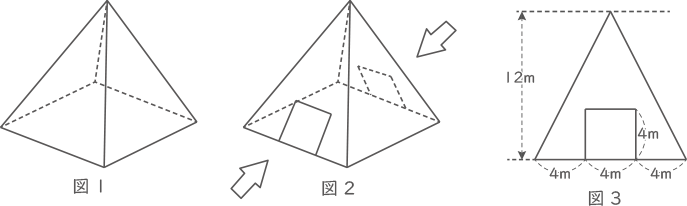
ある土地に、図1のような底面が正方形で、側面がすべて合同な二等辺三角形である四角すいの形に土が盛られています。この四角すいの底面の1辺は12mで、高さは12mです。このとき、次の各問いに答えなさい。ただし、円周率は3.14として計算しなさい。また、角すいの体積は、(底面積)×(高さ)÷3で求められます。
(1) 盛られている土の体積を求めなさい。
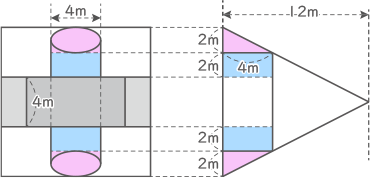
(2) この四角すいに、図3のように穴の形が1辺が4mの正方形である、入口から出口までまっすぐなトンネルを作りました。図2にはトンネルの2つの入口が記されています。図3は、これらの入口を図2の2つの矢印の方向から見た図です。このとき、トンネルを作る過程でほり出された土の体積を求めなさい。
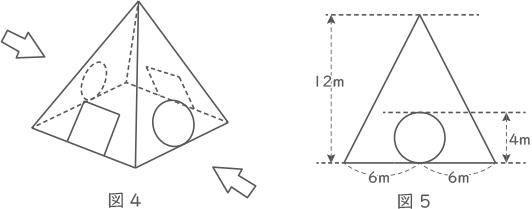
(3) さらに、図5のように穴の形が直径が4mの円である、入口から出口までまっすぐなトンネルを作りました。図4にはトンネルの4つの入口が記されています。図5は、これらの入口を図4の2つの矢印の方向から見た図です。このとき、新たにほリ出された土の体積を求めなさい。
これまでほとんどの通信教育で実現できなかった難関国私立中学合格。Z会なら、可能です。【公立中高一貫校を受検予定 】の方は試しに資料請求してみましょう。HPにも「小学生コース専科 公立中高一貫校受検対策講座のご案内」が詳しく記載されています。
解答
- 解答を開く
-
ある土地に、図1のような底面が正方形で、側面がすべて合同な二等辺三角形である四角すいの形に土が盛られています。この四角すいの底面の1辺は12mで、高さは12mです。このとき、次の各問いに答えなさい。ただし、円周率は3.14として計算しなさい。また、角すいの体積は、(底面積)×(高さ)÷3で求められます。
(1) 盛られている土の体積を求めなさい。
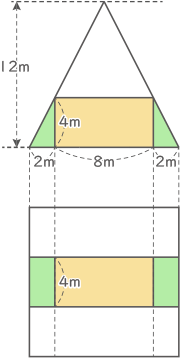
(2) この四角すいに、図3のように穴の形が1辺が4mの正方形である、入口から出口までまっすぐなトンネルを作りました。図2にはトンネルの2つの入口が記されています。図3は、これらの入口を図2の2つの矢印の方向から見た図です。このとき、トンネルを作る過程でほり出された土の体積を求めなさい。

(3) さらに、図5のように穴の形が直径が4mの円である、入口から出口までまっすぐなトンネルを作りました。図4にはトンネルの4つの入口が記されています。図5は、これらの入口を図4の2つの矢印の方向から見た図です。このとき、新たにほリ出された土の体積を求めなさい。

(1)
12×12×12×$ \displaystyle \frac{1}{3} $=576cm3(答え) 576cm3
 (2)
(2)
2×4×$ \displaystyle \frac{1}{2} $×4×2+4×4×8=160cm3(答え) 160cm3
(3)
(ピンクの立体は円柱を左右に等分したもの)
2×2×3.14×(2+2+2)=75.36cm3
(答え) 75.36cm3

 (2)
(2)