問題
下の各問いに答えなさい。
(円周率は3.14とする。)
(3辺の長さの比が3:4:5であるような三角形は、すべて直角三角形である。)
 (1)
(1)
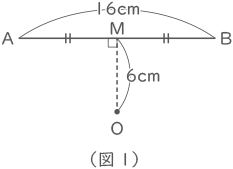
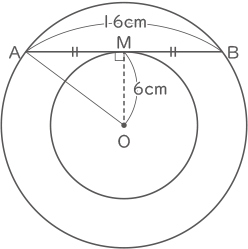
右の(図1)のように、長さ16cmのえんぴつABが机の上にあり、ABの真ん中の点をM とします。また、MO=6cmのところに点Oがあり、ABとMOは垂直です。このえんぴつを、点Oのまわりに机の上で1回転させたとき、えんぴつが通ってできる図形の面積は何cm2ですか。ただし、えんぴつの太さは考えないものとします。
以下、長方形の対角線の交点を、長方形の中心と呼ぶことにします。
 (2)
(2)
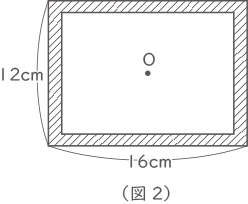
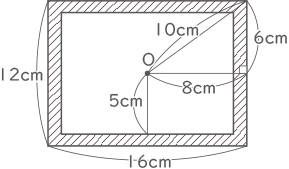
右の(図2)のように、縦12cm,横16cm,わくのはば1cmの長方形の額ぶちが机の上にあります。この額ぶちを、額ぶちの中心Oのまわりに机の上で1回転させたとき、わくが通ってできる図形の面積は何cm2ですか。
 (3)
(3)
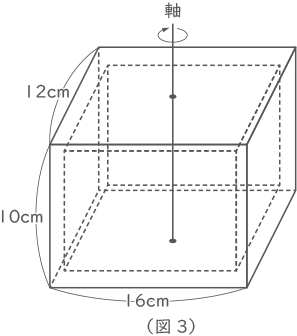
右の(図3) のように、厚さ1cmの長方形の板を6枚組み合わせて作った、中身が空どうの箱が机の上にあります。この箱を、上下の面の中心を通る直線を回転の軸(じく)として机の上で1回転させたとき、この箱の板の部分が通ってできる立体の体積は何cm3ですか。
灘をはじめ、名だたる難関中学に毎年多数の合格者を出す「浜学園」。講師の質や、教材のよさは折り紙付き。引きつりそうな料金設定ですが、中学受験をすると決めたら偏差値を買うんだ!ぐらいの前向きな気持ちで行きましょう。気になる方は資料請求してお子さんに合いそうか是非確認してみましょう。もちろん、体験入塾も無料で用意されています。
解答
- 解答を開く
-
下の各問いに答えなさい。
(円周率は3.14とする。)
(3辺の長さの比が3:4:5であるような三角形は、すべて直角三角形である。) (1)
(1)
右の(図1)のように、長さ16cmのえんぴつABが机の上にあり、ABの真ん中の点をM とします。また、MO=6cmのところに点Oがあり、ABとMOは垂直です。このえんぴつを、点Oのまわりに机の上で1回転させたとき、えんぴつが通ってできる図形の面積は何cm2ですか。ただし、えんぴつの太さは考えないものとします。以下、長方形の対角線の交点を、長方形の中心と呼ぶことにします。
 (2)
(2)
右の(図2)のように、縦12cm,横16cm,わくのはば1cmの長方形の額ぶちが机の上にあります。この額ぶちを、額ぶちの中心Oのまわりに机の上で1回転させたとき、わくが通ってできる図形の面積は何cm2ですか。 (3)
(3)
右の(図3) のように、厚さ1cmの長方形の板を6枚組み合わせて作った、中身が空どうの箱が机の上にあります。この箱を、上下の面の中心を通る直線を回転の軸(じく)として机の上で1回転させたとき、この箱の板の部分が通ってできる立体の体積は何cm3ですか。 (1)
(1)
3辺の長さの比が3:4:5であれば直角三角形となるのでOM:MA:AO=6:8:10, AO=10cm
10×10×3.14-6×6×3.14=200.96cm2(答え) 200.96cm2
 (2)
(2)
(1)と同様に比を考えると、小さい円の半径は5cm、大きい円の半径は10cmとなる。
10×10×3.14-5×5×3.14=235.5cm2(答え) 235.5cm2
(3)
長さが同じなので(2)の答えが利用できる。
回転させた際に内部が空洞になる部分の円柱の高さは8cmであり、また、その部分の体積は、
235.5×8=1884cm3
上下の高さ1cmの円柱の体積は、
10×10×3.14×1×2=628cm3
合わせて、
1884+628=2512cm3(答え) 2512cm3

 (1)
(1) (2)
(2)