問題
問題(専修大学松戸中学2016/最大公約数と最小公倍数の関係がわかっていれば解ける問題)
異なる3つの整数A,B,Cがあります。A,B,Cの和は90で,A,B,Cの最大公約数は10です。このとき,A,B,Cの最小公倍数として考えられる数は,[ ],[ ],[ ]の3つあります。
【家庭学習】問題集の画像も大きく見えて小さい文字もきれい
4.35
Amazonブランドのタブレット[Fire HD 10 Plus タブレット10.1インチ]フルHDディスプレイ(1920×1200)だから広くて見やすく家勉の必需品。
解答
- 解答を開く
-
異なる3つの整数A,B,Cがあります。A,B,Cの和は90で,A,B,Cの最大公約数は10です。このとき,A,B,Cの最小公倍数として考えられる数は,[ ],[ ],[ ]の3つあります。
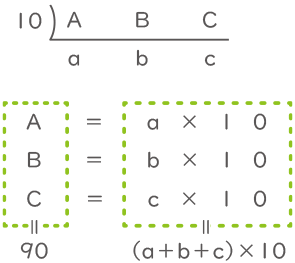
A、B、Cを最大公約数10で割った商をa、b、cとする。

90=(a+b+c)×10なので、a+b+c=9となる(a,b,c)の組み合わせを考える。(a,b,c)の組み合わせ
(1,1,7)・・・異なる3つの整数にならない(×)
(1,2,6)・・・異なる3つの整数で、最大公約数も10になる(○)
(1,3,5)・・・異なる3つの整数で、最大公約数も10になる(○)
(1,4,4)・・・異なる3つの整数にならない(×)
(2,2,5)・・・異なる3つの整数にならない(×)
(2,3,4)・・・異なる3つの整数で、最大公約数も10になる(○)
(3,3,3)・・・異なる3つの整数にならず、最大公約数が30になる(×)(A,B,C)の組み合わせ
(10,20,60)・・・最小公倍数60
(10,30,50)・・・最小公倍数150
(20,30,40)・・・最小公倍数120(答え) 60、120、150
ではまた~