問題
下の図のような1辺が10cmの正方形ABCDと,辺CDを両側に5cmずつ延長した直線EFがあります。
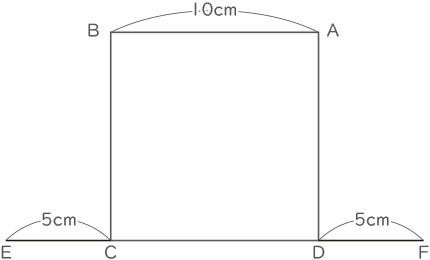
この図形上を2点P,Qが同時に出発して,一定の速さで移動します。点Pは,点Aを出発して,正方形ABCDの辺上をA→B→C→D→A →B→・・・の順に繰り返し移動します。また,点Qは点Eを出発して,直線EF上をE→F→E→F→・・・と往復します。
このとき,次の問いに答えなさい。
(1)点Pが毎秒2cm,点Qが毎秒5cmで移動するとき,点Pと点Qが初めて重なるのは,2点が出発してから[ア]秒後,2回目に重なるのは[イ]秒後です。[ア],[イ]にあてはまる数をそれぞれ答えなさい。
(2)点Pが毎秒2cm,点Qは点Pよりも速い速さで移動する場合について考えます。点Qが毎秒[ウ] cmよりも速く,毎秒[エ]cmよりも遅い速さで移動するときに限り,点Pが1回目に点C,Dを含む辺CD上を移動するときに,点Q と重なることはありません。[ウ],[エ]にあてはまる数をそれぞれ答えなさい。
(3)点Pが毎秒2cm,点Qは毎秒2cmよりも速く,毎秒4cmよりも遅い速さで移動する場合について考えます。点Pが1回目に辺CD上を移動する間に点Q と重なることがあり,点Pが2回目に点D に重なるとき,点Qも同時に点Dに重なります。このとき,点Qの移動する速さは毎秒[オ]cm です。[オ]にあてはまる数として考えられるものをすべて答えなさい。
人里離れた旅館?それとも海辺のリゾートホテル? 中学受験の前に一区切り、受験前最後の家族旅行はお早めに。今がそのチャンスかも。
解答
- 解答を開く
-
下の図のような1辺が10cmの正方形ABCDと,辺CDを両側に5cmずつ延長した直線EFがあります。

この図形上を2点P,Qが同時に出発して,一定の速さで移動します。点Pは,点Aを出発して,正方形ABCDの辺上をA→B→C→D→A →B→・・・の順に繰り返し移動します。また,点Qは点Eを出発して,直線EF上をE→F→E→F→・・・と往復します。
このとき,次の問いに答えなさい。
(1)点Pが毎秒2cm,点Qが毎秒5cmで移動するとき,点Pと点Qが初めて重なるのは,2点が出発してから[ア]秒後,2回目に重なるのは[イ]秒後です。[ア],[イ]にあてはまる数をそれぞれ答えなさい。
(2)点Pが毎秒2cm,点Qは点Pよりも速い速さで移動する場合について考えます。点Qが毎秒[ウ] cmよりも速く,毎秒[エ]cmよりも遅い速さで移動するときに限り,点Pが1回目に点C,Dを含む辺CD上を移動するときに,点Q と重なることはありません。[ウ],[エ]にあてはまる数をそれぞれ答えなさい。
(3)点Pが毎秒2cm,点Qは毎秒2cmよりも速く,毎秒4cmよりも遅い速さで移動する場合について考えます。点Pが1回目に辺CD上を移動する間に点Q と重なることがあり,点Pが2回目に点D に重なるとき,点Qも同時に点Dに重なります。このとき,点Qの移動する速さは毎秒[オ]cm です。[オ]にあてはまる数として考えられるものをすべて答えなさい。
(1)
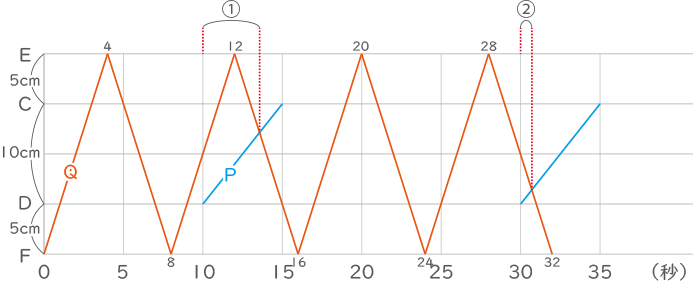
ECDF間のダイヤグラムを作る。
①の時間に点Qと点Pの進む距離の合計は25cm。
よって、求める時間アは10+$ \displaystyle \frac{25}{2+5} $=13$ \displaystyle \frac{4}{7} $秒
②の時間に点Qと点Pの進む距離の合計は5cm。
よって、求める時間イは30+$ \displaystyle \frac{5}{2+5} $=30$ \displaystyle \frac{5}{7} $秒
(答え) ア 13$ \displaystyle \frac{4}{7} $ イ 30$ \displaystyle \frac{5}{7} $
(2)
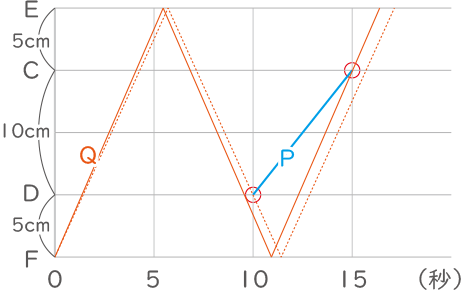
点Qが実線より速く、そして点線より遅く動く時が今回の条件にあてはまる。点線から、35÷10=3.5cm/sより速く、
実線から、55÷15=3$ \displaystyle \frac{2}{3} $cm/sより遅くなればよい。

(答え) ウ 3.5 エ 3$ \displaystyle \frac{2}{3} $
(3)
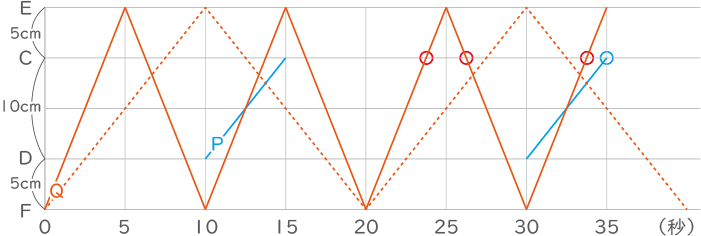
赤い実線は点Qが4cm/sで移動するとき。
赤い点線は点Qが2cm/sで移動するとき。
赤い実線の移動速度を徐々に遅くすると赤い点線に重なる。そして重なるまでに赤い3つの○は青い○に重なる。
条件にあてはまる速度は、赤い3つの○が青い○に重なった速度。
95÷35=2$ \displaystyle \frac{5}{7} $cm/s
105÷35=3cm/s
135÷35=3$ \displaystyle \frac{6}{7} $cm/s
(答え) オ 2$ \displaystyle \frac{5}{7} $ ,3 ,3$ \displaystyle \frac{6}{7} $