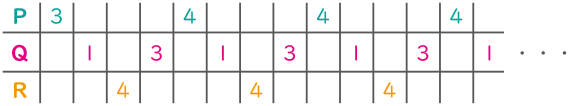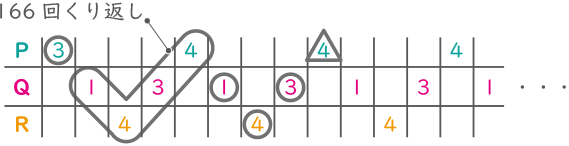
問題
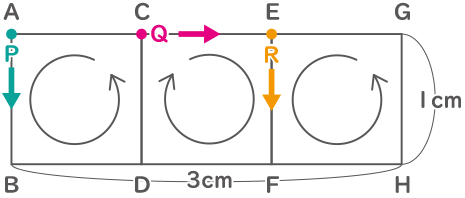
1辺が1cmの正方形を図の様にピッタリと並べました。その各正方形の辺上を点P、Q、Rが同じ秒速1cmで動きます。点Pは正方形ABDCの辺上を頂点Aから反時計回りに、点Qは正方形CDFEの辺上を頂点Cから時計回りに、点Rは正方形EFHGの辺上を頂点Eから反時計回りに、下記のルールにしたがって動きます。
【ルール:始めに1点が動き出し、となりの点に重なると動いていた点は止まり、重なったもう一方の点が動き出します。動き出した点がとなりの点に重なると止まり、重なったもう一方の点が動き出すことをくり返します。】
始めに点Pが動き出します。2004秒後の点P、Q、Rの動いた長さを一番簡単な整数比で求めなさい。
人里離れた旅館?それとも海辺のリゾートホテル? 中学受験の前に一区切り、受験前最後の家族旅行はお早めに。今がそのチャンスかも。
解答
- 解答を開く
-
1辺が1cmの正方形を図の様にピッタリと並べました。その各正方形の辺上を点P、Q、Rが同じ秒速1cmで動きます。点Pは正方形ABDCの辺上を頂点Aから反時計回りに、点Qは正方形CDFEの辺上を頂点Cから時計回りに、点Rは正方形EFHGの辺上を頂点Eから反時計回りに、下記のルールにしたがって動きます。
【ルール:始めに1点が動き出し、となりの点に重なると動いていた点は止まり、重なったもう一方の点が動き出します。動き出した点がとなりの点に重なると止まり、重なったもう一方の点が動き出すことをくり返します。】
始めに点Pが動き出します。2004秒後の点P、Q、Rの動いた長さを一番簡単な整数比で求めなさい。
点P、Q、Rをルール通りに動かして、動いた長さを点ごとに表にまとめる。

各点の規則性が分かる。1→4→3→4で1まとまりにできる。

2004÷(1+4+3+4)=167で割り切れるが点Pの初めが3なので12×166+12とし、12秒を点Pの3秒と、点Qの1秒・3秒、点Rの4秒に分け、残った1秒が点Pの△4にくる。
よって、3点の動いた長さは、
点P=3+4×166+1(△)=668
点Q=(1+3)×166+1+3=668
点R=4×166+4=668(答え)点P:点Q:点R=1:1:1