問題
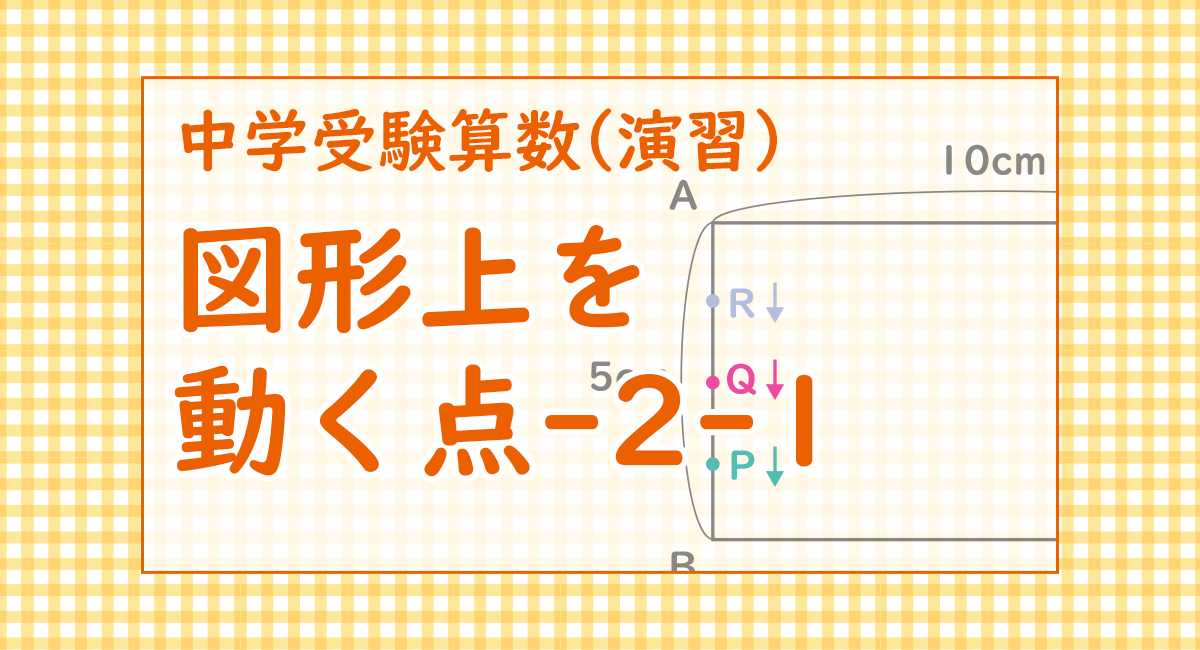
問題(長方形の辺上を動く3点)
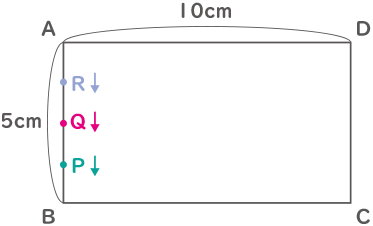
図の様な長方形があり、辺に沿って点P、点Q、点Rが頂点Aから同時に動き出します。3点の動く速さは、点Pが秒速10cm、点Qが秒速7cm、点Rが秒速2cmです。
(1) 点Rが2周して頂点Aにきたとき、点Pは点Qを何回追いこしましたか。
(2) 点Pが点Rに7回追いついたとき、点Qは点Rを何回追いこしましたか。
【家庭学習】問題集の画像も大きく見えて小さい文字もきれい
4.35
Amazonブランドのタブレット[Fire HD 10 Plus タブレット10.1インチ]フルHDディスプレイ(1920×1200)だから広くて見やすく家勉の必需品。
解答
- 解答を開く
-
図の様な長方形があり、辺に沿って点P、点Q、点Rが頂点Aから同時に動き出します。3点の動く速さは、点Pが秒速10cm、点Qが秒速7cm、点Rが秒速2cmです。
(1) 点Rが2周して頂点Aにきたとき、点Pは点Qを何回追いこしましたか。
(2) 点Pが点Rに7回追いついたとき、点Qは点Rを何回追いこしましたか。

(1)
点Rが2周すると30×2=60cm動き、60÷2=30秒かかる。30秒間に点Pと点Qの動いた差は(10-7)×30=90cm。動いた差30cmごとに点Pは点Qに追いつくので90÷30=3回追いつく。ただし、30秒後は2点が重なっているので追いこしたのは2回。(答え)2回
(2)
【点Pが点Rに7回追いつく=点Pが点Rより7周多くなる】ときなので、30×7÷(10-2)=26.25より、3点が動き出してから26.25秒後に7回追いつく。
また、点Qが点Rに1回追いつくには30÷(7-2)=6秒かかるので、26.25秒間に26.25÷6=4.3・・より4回追いこした。(答え)4回
ではまた~