問題
半径6cm,高さ35cmの円柱の容器に,底面から15cmの高さまで水が入っています。この中に半径2cm,高さ25cmの円柱の鉄の棒を1本ずつまっすぐに立てて入れていきます。
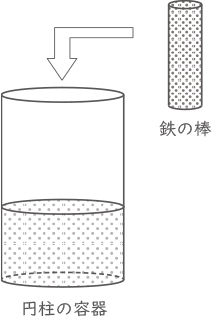
(1) 鉄の棒を1本入れたとき,水面は何cm上昇(じょうしょう)しますか。
(2) 入れた鉄の棒のすべてが,初めて完全に水の中に入るのは,鉄の棒を何本入れたときですか。また,そのときの水面の高さを求めなさい。
教室には遠くて通えない、通塾負担を減らしたい。もしくは他の習い事が忙しくて、通塾の時間が取れない・・・ そんなご家庭に最適! 4大塾に通いながら弱点補強を家庭教師に任せているご家庭も多々、塾のクラスを上げるためにピンポイントでうまく利用しましょう。なにはともあれ資料請求してお子さんに合うか見てみましょう。
解答
- 解答を開く
-
半径6cm,高さ35cmの円柱の容器に,底面から15cmの高さまで水が入っています。この中に半径2cm,高さ25cmの円柱の鉄の棒を1本ずつまっすぐに立てて入れていきます。

(1) 鉄の棒を1本入れたとき,水面は何cm上昇(じょうしょう)しますか。
(2) 入れた鉄の棒のすべてが,初めて完全に水の中に入るのは,鉄の棒を何本入れたときですか。また,そのときの水面の高さを求めなさい。
(1)
容器の底面積:鉄の棒の底面積=6×6×3.14:2×2×3.14=36:4=9:1
はじめの容器の底面積:鉄の棒を入れたときの容器の底面積=9:8
底面積と水位は逆比の関係にあるので、
はじめの容器の水位:鉄の棒を入れたときの容器の水位=8:9=15cm:□
□×8=15×9
□=16$ \displaystyle \frac{7}{8} $cm
16$ \displaystyle \frac{7}{8} $-15=1$ \displaystyle \frac{7}{8} $cm(答え) 1$ \displaystyle \frac{7}{8} $cm
(2)
【はじめに本数の計算】
鉄の棒の高さ:はじめの容器の水位=25:15=5:3=㊺:㉗
はじめの容器の底面積:鉄の棒を□本入れたときの容器の底面積=9:▲=㊺:△水位の比㉗よりも、鉄の棒を何本か入れたときの容器の底面積の比△が小さくなれば良く、比較のため両方を㊺に合わせる。
はじめの容器の底面積:鉄の棒を1本入れたときの容器の底面積=9:8=㊺:㊵
はじめの容器の底面積:鉄の棒を2本入れたときの容器の底面積=9:7=㊺:㉟
はじめの容器の底面積:鉄の棒を3本入れたときの容器の底面積=9:6=㊺:㉚
はじめの容器の底面積:鉄の棒を4本入れたときの容器の底面積=9:5=㊺:㉕
4本入れると㉗より小さくなり、水位が鉄の棒の高さを超える。よって、鉄の棒を4本入れたとき。【次に高さの計算】
はじめの容器の底面積は㊺で水位は15cmより、その水量は㊺×15=まる675。
鉄の棒を4本入れたときの容器の底面積は㉕で水位25cmまでの水量は㉕×25=まる625
鉄の棒の高さ25cmを超えた水量は、まる675-まる625=㊿
これを、はじめの容器の底面積㊺で割り、㊿÷㊺=1$ \displaystyle \frac{1}{9} $cmが鉄の棒より上の水位。
求める水位は、25+1$ \displaystyle \frac{1}{9} $=26$ \displaystyle \frac{1}{9} $cm。(答え) 4本 , 26$ \displaystyle \frac{1}{9} $cm