問題
[図1]のように底面の半径が6cm、高さが6cmの円柱の形をした容器の深さ4cmのところまで水が入っています。この水の中に[図2]のような底面の半径が2cm、高さが6cmの円柱から、底面の半径が1cm、高さが6cmの円柱をくり抜いた立体Aを入れます。このとき、後の問いに答えなさい。ただし、円周率は3.14とします。
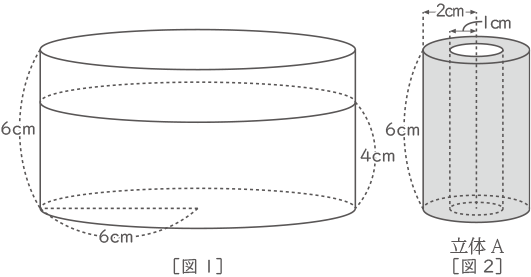
(1) 立体Aの体積は何cm3ですか。
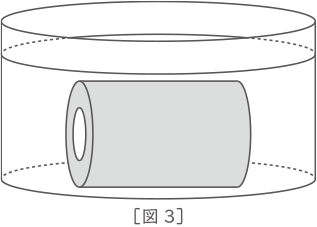
(2) [図3]のように、水の中に立体Aを横に倒(たお)して沈(しず)めます。このとき、水面の高さは何cmになりますか。
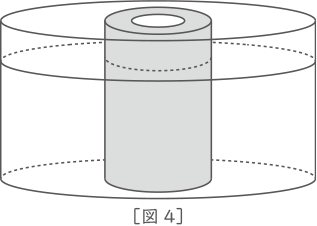
(3) 水の中に立体Aを縦にして、くり抜いた部分にも水が入るようにゆっくりと沈めていき、[図4]のように立体Aの底面が容器の底面についた状態に立てます。このとき、水面の高さは何cmになりますか。
教室には遠くて通えない、通塾負担を減らしたい。もしくは他の習い事が忙しくて、通塾の時間が取れない・・・ そんなご家庭に最適! 4大塾に通いながら弱点補強を家庭教師に任せているご家庭も多々、塾のクラスを上げるためにピンポイントでうまく利用しましょう。なにはともあれ資料請求してお子さんに合うか見てみましょう。
解答
- 解答を開く
-
[図1]のように底面の半径が6cm、高さが6cmの円柱の形をした容器の深さ4cmのところまで水が入っています。この水の中に[図2]のような底面の半径が2cm、高さが6cmの円柱から、底面の半径が1cm、高さが6cmの円柱をくり抜いた立体Aを入れます。このとき、後の問いに答えなさい。ただし、円周率は3.14とします。

(1) 立体Aの体積は何cm3ですか。
(2) [図3]のように、水の中に立体Aを横に倒(たお)して沈(しず)めます。このとき、水面の高さは何cmになりますか。
(3) 水の中に立体Aを縦にして、くり抜いた部分にも水が入るようにゆっくりと沈めていき、[図4]のように立体Aの底面が容器の底面についた状態に立てます。このとき、水面の高さは何cmになりますか。

(1)
(2×2×3.14-1×1×3.14)×6=3×6×3.14=56.52cm3(答え) 56.52cm3
(2)
(もとから入っている水の高さは4cmで、立体Aの直径も4cmなので立体Aは全て水に沈む。)
容器の底面積は(6×6×3.14)cm2
立体Aの体積は(3×6×3.14)cm3
増える水の高さは(3×6×3.14)÷(6×6×3.14)=0.5cm
水面の高さは4+0.5=4.5cm(答え) 4.5cm
(3)
(立体Aの高さ4cm分の体積が、容器の水の4cmより上に移動する。)
容器の底面積は(6×6×3.14)cm2
立体Aの底面積は2×2×3.14-1×1×3.14=(3×3.14)cm2
容器の水の4cmより上の水面の面積は(6×6×3.14)-(3×3.14)=(33×3.14)cm2
立体Aの体積の$ \displaystyle \frac{4}{6} $は(3×3.14×6×$ \displaystyle \frac{4}{6} $)=(12×3.14)cm3
増える水の高さは(12×3.14)÷(33×3.14)=$ \displaystyle \frac{12}{33} $=$ \displaystyle \frac{4}{11} $cm
水面の高さ=4+$ \displaystyle \frac{4}{11} $=4$ \displaystyle \frac{4}{11} $cm(答え) 4$ \displaystyle \frac{4}{11} $cm