問題
次の問いに答えなさい。
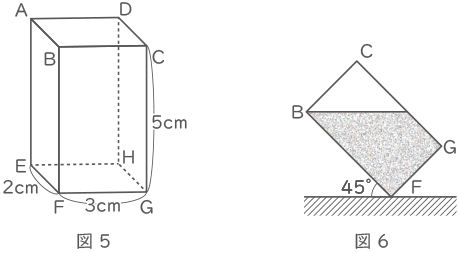
(1) 図5のように縦2cm, 横3cm,高さ5cmの直方体の容器があります。
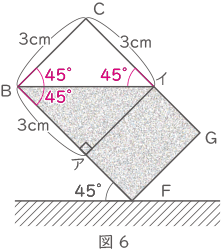
この容器いっぱいに水を入れ,図6のように辺EFを床につけた状態でこの容器を45゜傾けました。容器の中に残った水の体積は何cm3ですか。
(2) 図7の直方体の容器は体積が360cm3で,辺QUの長さは辺QRの長さの3倍です。
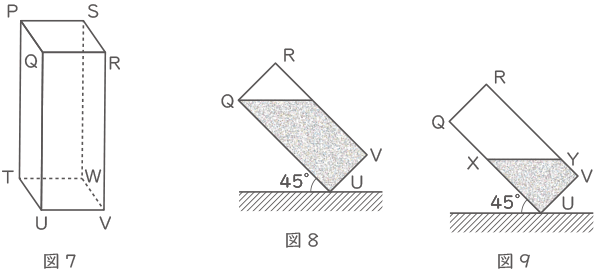
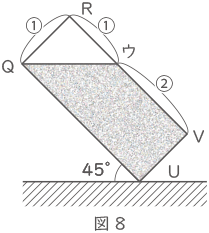
① 図7の容器いっぱいに水を入れ,図8のように辺TUを床につけた状態でこの容器を45゜傾けました。容器の中に残った水の体積は何cm3ですか。
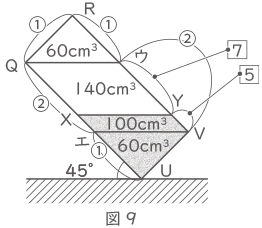
② 図8の状態から水をいくらか捨てて,再び辺TUを床につけた状態で,この容器を45゜傾けると, 図9のようになりました。容器の中に残った水の体積が160cm3のとき, QXとXUの長さの比を最も簡単な整数の比で求めなさい。
Amazonブランドのタブレット[Fire HD 10 Plus タブレット10.1インチ]フルHDディスプレイ(1920×1200)だから広くて見やすく家勉の必需品。
解答
- 解答を開く
-
次の問いに答えなさい。
(1) 図5のように縦2cm, 横3cm,高さ5cmの直方体の容器があります。
この容器いっぱいに水を入れ,図6のように辺EFを床につけた状態でこの容器を45゜傾けました。容器の中に残った水の体積は何cm3ですか。
(2) 図7の直方体の容器は体積が360cm3で,辺QUの長さは辺QRの長さの3倍です。

① 図7の容器いっぱいに水を入れ,図8のように辺TUを床につけた状態でこの容器を45゜傾けました。容器の中に残った水の体積は何cm3ですか。
② 図8の状態から水をいくらか捨てて,再び辺TUを床につけた状態で,この容器を45゜傾けると, 図9のようになりました。容器の中に残った水の体積が160cm3のとき, QXとXUの長さの比を最も簡単な整数の比で求めなさい。
(1)
辺BCと平行な点イを通るアイをつくる。
【考え方1】
四角形BCイアは正方形なので、これを底面積と考え、高さを辺ABとした直方体の体積の半分が、こぼれた水の容量となる。
【考え方2】
三角形BCイを底面積として、高さをABとした三角柱の体積が、こぼれた水の容量となる。
容器の容量-こぼれた水の容量=2×3×5-3×3÷2×2=21
(答え) 21cm3
(2)ー①

四角形QRVUの面積を①×③=③とすると、三角形QRウの面積は①×①÷2=①/2(ニブンノイチマル)
よって、四角形QRVUの面積:三角形QRウの面積=6:1となり、体積比も同じ。
容器の体積:容器の中に残った水の体積=6:5=360:300
容器の中に残った水の体積は300cm3(答え) 300cm3
(2)ー②

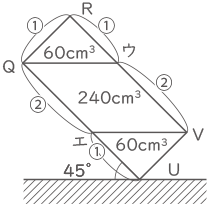
(2)ー①より、水のこぼれた三角形QRウの体積は60cm3、同じく三角形UVエも60cm3、四角形QウVエが残りの240cm3となる。

図の様に、
平行四辺形QウVエの体積は240cm3、
平行四辺形QウYXの体積は140cm3、
平行四辺形YXVエの体積は100cm3、
これより、QX:Xエ=140:100=$ \fbox{7} $:$ \fbox{5} $
Qエの長さを$ \fbox{12} $(=$ \fbox{7} $+$ \fbox{5} $)とすると、エUの長さは半分なので$ \fbox{6} $となる。
QX:Xエ:エU=$ \fbox{7} $:$ \fbox{5} $:$ \fbox{6} $とわかり、
QX:XU=$ \fbox{7} $:$ \fbox{5+6} $=$ \fbox{7} $:$ \fbox{11} $と求まる。(答え) 7 : 11