問題
つまようじを何本か使って立方体を組み立てます。はじめに,下の図の一番左のような立方体をつくったとき,必要なつまようじの本数は12本で,これを1段目とします。次に,縦,横,奥に1本ずつのばしてつくった立方体を2段目,3段目…とします。
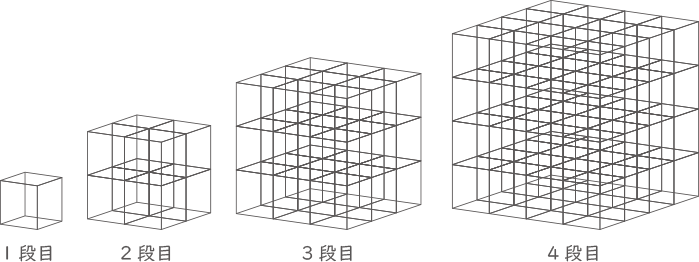
ここで,4段目の立方体に必要なつまようじの本数を考えます。縦,横,奥にそれぞれに分けて必要な本数を考えたとき,縦に必要なつまようじは,4×5×5=100(本)になります。さらに,横,奥も同じように数えることができるため,4段目に必要なつまようじの本数は,全部で4×5×5×3=300(本)になります。
次の問いに答えなさい。
(1) 5段目の立方体に必要なつまようじは何本ですか。
(2) 必要なつまようじの本数が2700本になるときの立方体は何段目ですか。
(3) 必要なつまようじの本数が100の倍数になるのは,1段目から100段目の中で,全部で何通りありますか。
教室には遠くて通えない、通塾負担を減らしたい。もしくは他の習い事が忙しくて、通塾の時間が取れない・・・ そんなご家庭に最適! 4大塾に通いながら弱点補強を家庭教師に任せているご家庭も多々、塾のクラスを上げるためにピンポイントでうまく利用しましょう。なにはともあれ資料請求してお子さんに合うか見てみましょう。
解答
- 解答を開く
-
つまようじを何本か使って立方体を組み立てます。はじめに,下の図の一番左のような立方体をつくったとき,必要なつまようじの本数は12本で,これを1段目とします。次に,縦,横,奥に1本ずつのばしてつくった立方体を2段目,3段目…とします。

ここで,4段目の立方体に必要なつまようじの本数を考えます。縦,横,奥にそれぞれに分けて必要な本数を考えたとき,縦に必要なつまようじは,4×5×5=100(本)になります。さらに,横,奥も同じように数えることができるため,4段目に必要なつまようじの本数は,全部で4×5×5×3=300(本)になります。
次の問いに答えなさい。
(1) 5段目の立方体に必要なつまようじは何本ですか。
(2) 必要なつまようじの本数が2700本になるときの立方体は何段目ですか。
(3) 必要なつまようじの本数が100の倍数になるのは,1段目から100段目の中で,全部で何通りありますか。(1)
設問の式と同様に他の段も式を作る。
1段目:1×2×2×3
2段目:2×3×3×3
3段目:3×4×4×3
4段目:4×5×5×3
この規則性より、
□段目:□×(□+1)×(□+1)×3
となる。よって、
5段目:5×6×6×3=540(答え) 540本
(2)
□段目:□×(□+1)×(□+1)×3=2700
□×(□+1)×(□+1)=900
□=9(答え) 9段目
(3)
100の倍数 ⇒ 式の中に約数5が2つと約数2が2つ含まれればよい。【□段目:□×(□+1)×(□+1)×3の(□+1)が5の倍数のものを数える】
4段目:4×(5×1)×(5×1)×3・・・〇
9段目:9×(5×2)×(5×2)×3・・・〇
14段目:14×(5×3)×(5×3)×3・・・×
19段目:19×(5×4)×(5×4)×3・・・〇
24段目:24×(5×5)×(5×5)×3・・・〇
29段目:29×(5×6)×(5×6)×3・・・〇
34段目:34×(5×7)×(5×7)×3・・・×
…
以上より、9を含む段は全て条件に当てはまるので9段目,19段目,…,99段目の10通り。・・・①4を含む段の残りを全て確認する。
44段目:44×(5×9)×(5×9)×3・・・〇
54段目:54×(5×11)×(5×11)×3・・・×
64段目:64×(5×13)×(5×13)×3・・・〇
74段目:74×(5×15)×(5×15)×3・・・×
84段目:84×(5×17)×(5×17)×3・・・〇
94段目:94×(5×19)×(5×19)×3・・・×
以上より、4を含む段は条件に当てはまるのは5通り。・・・②【□段目:□×(□+1)×(□+1)×3の□が25の倍数のものを数える】
25段目:25×26×26×3・・・〇
50段目:50×51×51×3・・・×
75段目:75×76×76×3・・・〇
100段目:100×99×99×3・・・〇
以上より、条件に当てはまるのは3通り。・・・③①+②+③=18通り。
(答え) 18通り

![樹形図-1-4(恵泉女学園中学2022/[し],[ん],[ぶ],[ん],[し]を並べかえて文字の列を作ります)](https://chuju-sansu.takaibiki.com/wp-content/uploads/2022/11/173d63142af659780fe3c2f376a580c1-375x203.png)








