問題
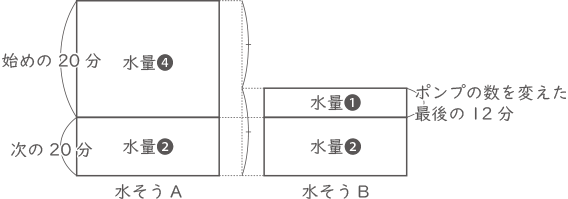
水の入っている水そうAと水そうB,そして,水を汲(く)みだすためのポンプが何本かあリます。また,水そうAに入っている水の量は水そうBに入っている水の量の2倍です。
はじめの20分は,全てのポンプを使って水そうAの水を汲みだします。
次に,ポンプの数をちょうど半分ずつに分け,半分で水そうAの水を,もう半分で水そうBの水を汲みだします。すると,ちょうど20分で水そうAのすべての水を汲みだすことができましたが,水そうBにはまだ水が残っていました。
そこで,ポンプの数を変えて水そうBの水を汲みだすと,さらに12分で水そうBのすべての水を汲みだすことができました。
このとき,次の問いに答えなさい。
ただし,すべてのポンプとも1分あたりに汲みだす水の量は一定であるとします。
(1) 「汲みだす前の水そうAの水の量」に対する「はじめの20分で汲みだした水の量」を,もっとも簡単な分数で答えなさい。
(2) 最後の12分で汲みだした水をすべてのポンプを使って汲みだそうとすると,汲みだすのに何分かかリますか。
(3) ここまでの条件では,はじめにあったポンプの総数は決まリません。ここまでの条件をすべて満たすポンプの総数のなかで最も小さい数を答えなさい。ただし,途中の考え方も書きなさい。
四谷大塚の対面授業の指導力と、東進の映像制作技術を融合した東進オンライン学校。わかりやすくて面白いから、楽しみながら勉強が続けられます。 <オンラインなので全国どこからでも自宅で超一流の先生の授業を受けられます!しかも授業料は【格安】>
解答
- 解答を開く
-
水の入っている水そうAと水そうB,そして,水を汲(く)みだすためのポンプが何本かあリます。また,水そうAに入っている水の量は水そうBに入っている水の量の2倍です。
はじめの20分は,全てのポンプを使って水そうAの水を汲みだします。
次に,ポンプの数をちょうど半分ずつに分け,半分で水そうAの水を,もう半分で水そうBの水を汲みだします。すると,ちょうど20分で水そうAのすべての水を汲みだすことができましたが,水そうBにはまだ水が残っていました。
そこで,ポンプの数を変えて水そうBの水を汲みだすと,さらに12分で水そうBのすべての水を汲みだすことができました。
このとき,次の問いに答えなさい。
ただし,すべてのポンプとも1分あたりに汲みだす水の量は一定であるとします。(1) 「汲みだす前の水そうAの水の量」に対する「はじめの20分で汲みだした水の量」を,もっとも簡単な分数で答えなさい。
(2) 最後の12分で汲みだした水をすべてのポンプを使って汲みだそうとすると,汲みだすのに何分かかリますか。
(3) ここまでの条件では,はじめにあったポンプの総数は決まリません。ここまでの条件をすべて満たすポンプの総数のなかで最も小さい数を答えなさい。ただし,途中の考え方も書きなさい。 (1)
(1)
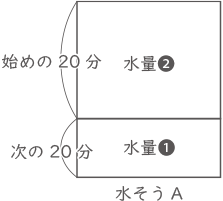
水そうAでは、はじめの20分と次の20分のポンプの本数比が2:1なので、水量比も❷:❶になる。
よって、汲みだす前の水そうAの水の量:はじめの20分で汲みだした水の量=❸:❷となり、$ \displaystyle \frac{2}{3} $(答え) $ \displaystyle \frac{2}{3} $
(2)
水そうAと水そうBの水量比をふりなおす。
全てのポンプで水量❹のときに20分かかるのであれば、水量❶では20÷4=5分。
(答え) 5分
(3)
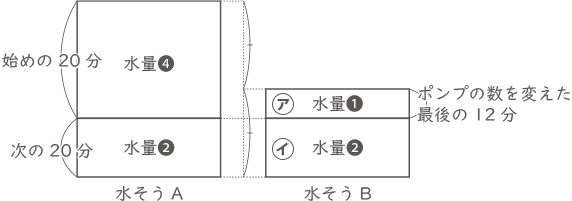
㋐と㋑で水量❶を汲みだす時間比は12分:10分=6:5
汲みだす水量比は逆比になり㋐:㋑=5:6、これをポンプの本数比と見ることができる。
最小の比は5本:6本で、ポンプの総数は6×2=12本。
(答え) 12本
別解(3)ポンプの総数は偶数なので少ない数から地道に数え上げる方法もある。
㋐と㋑が❷の水量を汲みだす時間は20分と24分なので、この数字で考える。【ポンプの総数が2本のとき】
㋑がポンプ1本のとき、㋐はそれより少なくできない・・・×
【ポンプの総数が4本のとき】
㋑がポンプ2本で20分のとき、㋐は1本で40分・・・×
【ポンプの総数が6本のとき】
㋑がポンプ3本で20分のとき、㋐は2本で30分、1本で60分・・・×
【ポンプの総数が8本のとき】
㋑がポンプ4本で20分のとき、㋐は3本で80/3分、2本で40分、以下略・・・×
【ポンプの総数が10本のとき】
㋑がポンプ5本で20分のとき、㋐は4本で25分、以下略・・・×
【ポンプの総数が12本のとき】
㋑がポンプ6本で20分のとき、㋐は5本で24分・・・○これより、ポンプの総数が12本のとき条件に当てはまる
(答え) 12本


 (1)
(1)