問題
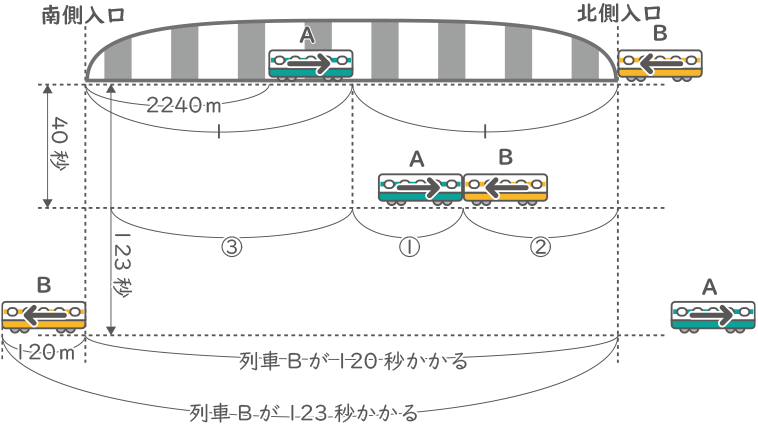
図は、列車Aが南側から、列車Bが北側から鉄橋を渡ろうとしていることろです。このあと、列車Aは先頭が鉄橋の真ん中に、最後尾が鉄橋の南側入口から2240mのところまで入り、同時に列車Bは先頭が鉄橋の北側入口に着きました。そこから40秒後に列車どうしが出会いました。また、列車Bが鉄橋を渡り始めてから渡り終わるまでは123秒かかりました。列車Bの長さは120mで、列車Aの倍の速さで走っています。列車Aの長さを求めなさい。

人里離れた旅館?それとも海辺のリゾートホテル? 中学受験の前に一区切り、受験前最後の家族旅行はお早めに。今がそのチャンスかも。
解答
- 解答を開く
-
図は、列車Aが南側から、列車Bが北側から鉄橋を渡ろうとしていることろです。このあと、列車Aは先頭が鉄橋の真ん中に、最後尾が鉄橋の南側入口から2240mのところまで入り、同時に列車Bは先頭が鉄橋の北側入口に着きました。そこから40秒後に列車どうしが出会いました。また、列車Bが鉄橋を渡り始めてから渡り終わるまでは123秒かかりました。列車Bの長さは120mで、列車Aの倍の速さで走っています。列車Aの長さを求めなさい。

列車Aの先頭が鉄橋の真ん中に来た時、列車Bの先頭は鉄橋の北側入口なので、2つの列車の先頭の距離は鉄橋の長さの半分となっている。
そこから40秒後に2つの列車が出会うが、列車Aの速さ:列車Bの速さ=1:2なので、列車Aの進んだ距離を①とすると列車Bの進んだ距離は②となり、鉄橋の長さは⑥となる。
列車Bは②の距離を40秒で走るので⑥の距離を走るには40×(⑥÷②)=40×3=120秒かかる。【鉄橋の長さ+列車Bの長さ】を列車Bは123秒で走るので、123-120=3秒で120m(列車Bの長さ)走る。
よって列車Bの速さは秒速40m。
鉄橋の長さは40×120=4800mで、列車Aの長さは4800÷2-2240=160mとなる。
(答え)160m