問題
次の図1,図2の時計について,以下の問いに答えなさい。
 (1)
(1)
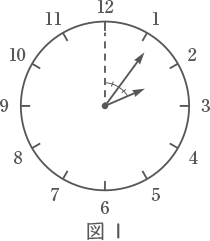
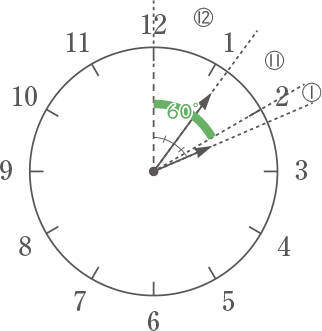
2時から3時までの1時間で,図1の点線と短針の間の角度が,長針によって2等分される時刻を答えなさい。ただし,秒の値のみ帯分数を用いて答えること。
 (2)
(2)
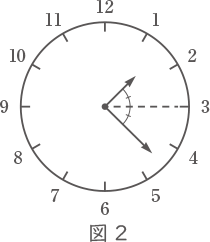
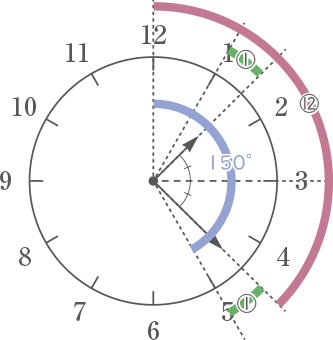
1時から2時までの1時間で,短針と長針の間の角度が,図2の点線によって2等分される時刻を答えなさい。ただし,秒の値のみ帯分数を用いて答えること。
人里離れた旅館?それとも海辺のリゾートホテル? 中学受験の前に一区切り、受験前最後の家族旅行はお早めに。今がそのチャンスかも。
解答
- 解答を開く
-
次の図1,図2の時計について,以下の問いに答えなさい。
 (1)
(1)
2時から3時までの1時間で,図1の点線と短針の間の角度が,長針によって2等分される時刻を答えなさい。ただし,秒の値のみ帯分数を用いて答えること。 (2)
(2)
1時から2時までの1時間で,短針と長針の間の角度が,図2の点線によって2等分される時刻を答えなさい。ただし,秒の値のみ帯分数を用いて答えること。 (1)
(1)
短針は1分間に0.5度、長針は1分間に6度進むでの、その比は1:12。
2等分される時刻を図の様に比で考えると、12時と長針の角度は⑫で、2時と短針の角度は①となり、12時と2時の角度60°が㉑となる。
よって、⑫は(60×$ \displaystyle \frac{12}{23} $)°
長針の時刻は60×$ \displaystyle \frac{12}{23} $×$ \displaystyle \frac{1}{6} $=5$ \displaystyle \frac{5}{23} $分
=5分$ \displaystyle \frac{300}{23} $秒=5分13$ \displaystyle \frac{1}{23} $秒(答え)2時5分13$ \displaystyle \frac{1}{23} $秒
 (2)
(2)
短針は1分間に0.5度、長針は1分間に6度進むので、その比は1:12。
2等分される時刻を図の様に比で考えると、1時から短針の進む角度を①とすると、長針の進む角度は⑫となる。また、長針と5時も①となる。12時から5時までの角度は⑬(=⑫+①)で150°なので、⑫=(150×$ \displaystyle \frac{12}{13} $)°
長針の時刻は(150×$ \displaystyle \frac{12}{13} $ )×$ \displaystyle \frac{1}{6} $=23$ \displaystyle \frac{1}{13} $分
=23分$ \displaystyle \frac{60}{13} $秒=23分4$ \displaystyle \frac{8}{13} $秒(答え)1時23分4$ \displaystyle \frac{8}{13} $秒

 (1)
(1) (2)
(2)








