旅人算-2-9（巣鴨中学2022/程よく難しい問題、比、連比、割合、いろいろ駆使して進めましょう）

問題

解答

 解答を開く

 

P地点からQ地点までまっすぐな道があリます。太郎君はP地点からQ地点へ向かって、次郎君と三郎君はQ地点からP地点へ向かって、3人とも同じ時刻に出発しました。太郎君は、出発してから30分後に次郎君と出会い、その1分30秒後に三郎君と出会いました。また、次郎君は太郎君と出会ってから40分後に、P地点に着きました。このとき、次の各問いに答えなさい。
ただし、答えが割リ切れないときは、最も簡単な分数で答えなさい。

（1） 太郎君と次郎君の速さの比を、最も簡単な整数の比で表しなさい。
（2） 三郎君は、出発してから何分後にP地点に着きますか。
（3） 太郎君のいる地点が、次郎君のいる地点と三郎君のいる地点のちょうど真ん中になるのは、出発してから何分後ですか。

 

---

 

（1）
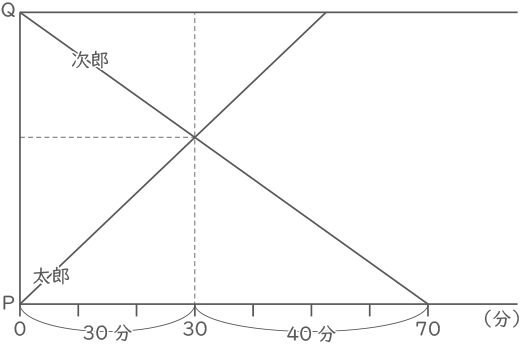
太郎と次郎は、下図の様に同じ距離を30分と40分で移動するので、かかる時間の比3：4の逆比4：3が速さの比。

（答え）　4：3

 

（2）
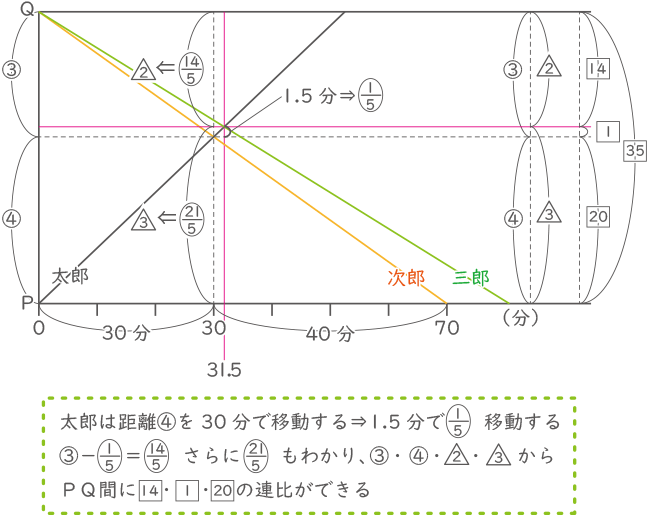
問（1）のことより、P地点～太郎と次郎の出会った地点～Q地点が④：③の比であることがわかった。

次郎は距離$ \fbox{35} $を70分かかるので、$ \fbox{1} $は2分かかる。
三郎は距離$ \fbox{14} $を31.5分かかるので、$ \fbox{1} $は2.25分かかる。
これより、同じ距離にかかる時間の比は次郎：三郎＝2：2.25＝8：9。
P地点に着く時間の比は次郎：三郎＝70分：□分＝8：9。
□＝$ \displaystyle \frac{70×9}{8} $＝78$ \displaystyle \frac{3}{4} $分

（答え）　78$ \displaystyle \frac{3}{4} $分後

 

（3）
＜次郎と三郎の中間の速さの四郎をつくり、太郎と四郎の出会い算を考えればよい＞
速さの比は、
太郎：次郎＝4：3・・・問（1）より
次郎：三郎＝9：8・・・問（2）のかかる時間の逆比より
連比にして、太郎：次郎：三郎＝12：9：8
よって、四郎の速さを中間の速さ（9＋8）÷2=8.5とする。
速さの比は、太郎：四郎＝12：8.5=㉔：⑰で、2人の速さを合わせると㊶。
求める時間は距離$ \fbox{35} $を㊶で割った$ \displaystyle \frac{\fbox{35} }{㊶} $。
＜太郎の動きからこれを求める＞
太郎は距離$ \fbox{20} $を速さ㉔で30分で移動する。
$ \fbox{20} $×$ \displaystyle \frac{1}{㉔} $＝30分

$ \fbox{20} $×$ \displaystyle \frac{35}{20} $×$ \displaystyle \frac{1}{㉔} $×$ \displaystyle \frac{24}{41} $×＝$ \displaystyle \frac{\fbox{35} }{㊶} $＝30分×$ \displaystyle \frac{35}{20} $×$ \displaystyle \frac{24}{41} $＝$ \displaystyle \frac{1260}{41} $＝30$ \displaystyle \frac{30}{41} $分

（答え）　30$ \displaystyle \frac{30}{41} $分後