問題
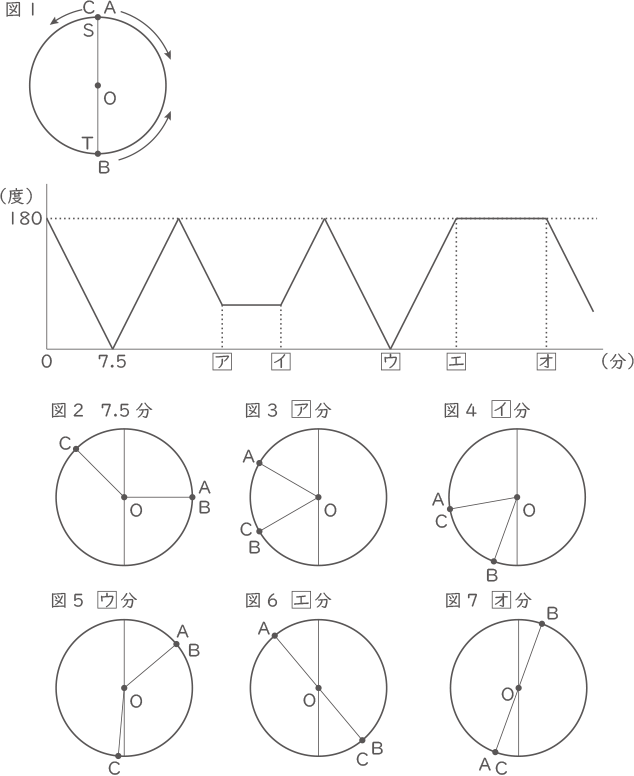
図1のように円周上に2点S,Tがあり,点Aと点CはSから,点BはTから同時に出発しそれぞれ一定の速さで動きます。点Aは右回りに,点Bと点Cは左回りに動き,点Aと点Bは点Cの2倍の速さで動きます。また, 3点A,B,Cは他の点と出会うと,それぞれ速さを変えずに逆向きに動きます。下のグラフは,この3点が出発してからの時間と2辺OAとOBが作る角の大きさの変化を表したものの一部です。ただし,2辺OAとOBが作る角の大きさは180゜以下とします。また,図2~図7は,3点A,B,Cのうち2つの点が出会ったときを順に表したものです。
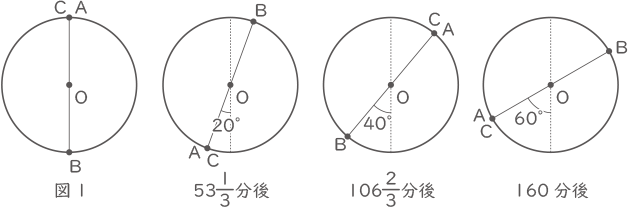
(1) 出発してから1分後の2辺OSとOCが作る角の大きさは何度ですか。180゜以下で答えなさい。
(2) $ \fbox{イ} $,$ \fbox{オ} $にあてはまる数を答えなさい。
(3) 3点A,B,Cが初めて図1の状態にもどるのは,出発してから何分後ですか。
Amazonブランドのタブレット[Fire HD 10 Plus タブレット10.1インチ]フルHDディスプレイ(1920×1200)だから広くて見やすく家勉の必需品。
解答
- 解答を開く
-
図1のように円周上に2点S,Tがあり,点Aと点CはSから,点BはTから同時に出発しそれぞれ一定の速さで動きます。点Aは右回りに,点Bと点Cは左回りに動き,点Aと点Bは点Cの2倍の速さで動きます。また, 3点A,B,Cは他の点と出会うと,それぞれ速さを変えずに逆向きに動きます。下のグラフは,この3点が出発してからの時間と2辺OAとOBが作る角の大きさの変化を表したものの一部です。ただし,2辺OAとOBが作る角の大きさは180゜以下とします。また,図2~図7は,3点A,B,Cのうち2つの点が出会ったときを順に表したものです。

(1) 出発してから1分後の2辺OSとOCが作る角の大きさは何度ですか。180゜以下で答えなさい。
(2) $ \fbox{イ} $,$ \fbox{オ} $にあてはまる数を答えなさい。
(3) 3点A,B,Cが初めて図1の状態にもどるのは,出発してから何分後ですか。(1)
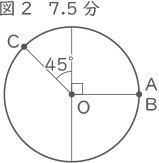
グラフより、7.5分で点A,B共に90°進むので1分では12°進む。
点Cはその半分の速さで進むので1分あたり6°進む。(答え) 6度
(2)
点A,Bの速さを②、点Cの速さを①として、図3~図7までの時間をうめてゆく。 6×7.5=45°
6×7.5=45° 150°=225×$ \displaystyle \frac{②}{③} $
150°=225×$ \displaystyle \frac{②}{③} $
150÷12=12.5
7.5+12.5=20分・・・ア 図3からAとCは60°の出会い算。
図3からAとCは60°の出会い算。
60×$ \displaystyle \frac{②}{③} $=40°がAの進んだ角度。
40÷12=3$ \displaystyle \frac{1}{3} $
20+3$ \displaystyle \frac{1}{3} $=23$ \displaystyle \frac{1}{3} $分・・・イ
また、角AOCは60°となり、これを図5で利用する。 図4で角AOCが60°になることから、図3から図2に動く時と、図4から図5へ動く時は左右対称のグラフになることを利用する。
図4で角AOCが60°になることから、図3から図2に動く時と、図4から図5へ動く時は左右対称のグラフになることを利用する。
23$ \displaystyle \frac{1}{3} $+20-7.5=35$ \displaystyle \frac{5}{6} $分・・・ウ
角度については図4よりABの出会い算を使い、
300×$ \displaystyle \frac{①}{②} $=150、150-(60+40)=50°
6×12.5=75、75+(60+40)=175° 図5から図6への動きの逆が図2から図1への動きなので、
図5から図6への動きの逆が図2から図1への動きなので、
35$ \displaystyle \frac{5}{6} $+7.5=43$ \displaystyle \frac{1}{3} $分・・・エ
12×7.5=90、90-50=40° 図6で角AOCが180°なので、ACの出会い算より、
図6で角AOCが180°なので、ACの出会い算より、
180×$ \displaystyle \frac{②}{③} $=120、40+120=160°
(160-40)÷12=10、43$ \displaystyle \frac{1}{3} $+10=53$ \displaystyle \frac{1}{3} $分・・・オ(答え) イ 23$ \displaystyle \frac{1}{3} $ オ 53$ \displaystyle \frac{1}{3} $
(3)
図の様に160分後に60°回転するので、あと120°回転すると元の位置に戻る。
180÷60=3、160×3=480分
(答え) 480分後


 6×7.5=45°
6×7.5=45°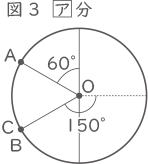 150°=225×$ \displaystyle \frac{②}{③} $
150°=225×$ \displaystyle \frac{②}{③} $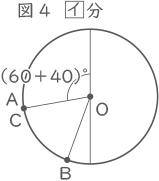 図3からAとCは60°の出会い算。
図3からAとCは60°の出会い算。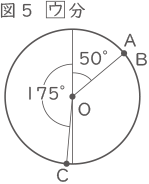 図4で角AOCが60°になることから、図3から図2に動く時と、図4から図5へ動く時は左右対称のグラフになることを利用する。
図4で角AOCが60°になることから、図3から図2に動く時と、図4から図5へ動く時は左右対称のグラフになることを利用する。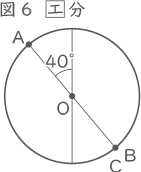 図5から図6への動きの逆が図2から図1への動きなので、
図5から図6への動きの逆が図2から図1への動きなので、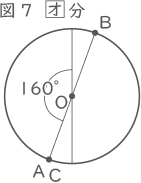 図6で角AOCが180°なので、ACの出会い算より、
図6で角AOCが180°なので、ACの出会い算より、