旅人算-2-6（攻玉社中学2022/（1）が難しく、これが解けないと後の問題に進めない）

問題

解答

 解答を開く

 

次の□にあてはまる数を求めなさい。

A，B，Cの3人が、学校と駅を結ぶ一本道を途中で引き返すことなく、それぞれ一定の速さで歩きます。8時ちょうどにAは学校から駅へ、Bは駅から学校へ向かって同時に出発し、9時48分にCはBの2倍の速さで駅から学校へ向かって出発しました。また、Aは9時ちょうどにBと、10時ちょうどにCとすれちがいました。CはAとすれちがったときに、その場で何分間か休んでから学校へ向かったところ、Aが駅に着くのと同時に、Cは学校に着きました。

（1） AとBの速さの比は□です。
（2） AがCとすれちがった地点から、AがBとすれちがった地点までの道のりを、Cは□分で歩きます。
（3） B が学校に着くのは□時□分です。
（4） Cが休んだ時間は□分間です。
（5） Bが学校に着いてからすぐに折り返して、それまでと同じ速さで駅に向かうとき、C と出会うのは□時□分□秒です。

 

---

 

問題に図が与えられていないので、自分でダイヤグラムを書くしかない、書けないとお手上げ・・・

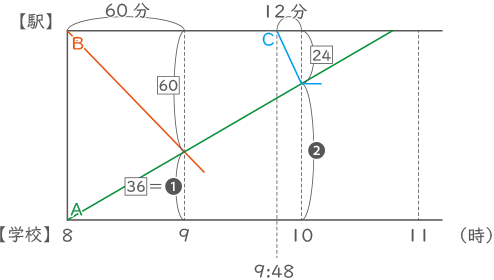
（1）
Bの分速を$\boxed{\text{1}}$とすると、Ｃは$\boxed{\text{2}}$となる。
Ａが60分で進む距離を❶とすると、120分では❷となる。
これを使って学校駅間の距離を表すと、
❶＋$\boxed{\text{1}}$×60分＝❷＋$\boxed{\text{2}}$×12分
❶＋$\boxed{\text{60}}$＝❷＋$\boxed{\text{24}}$
$\boxed{\text{36}}$＝❶
以上より、60分でAは$\boxed{\text{36}}$進み、Bは$\boxed{\text{60}}$進む。36：60＝3：5。

（答え）　3：5

 

（2）
対象となる道のりは❷－❶＝❶＝$\boxed{\text{36}}$で、Cの速さは分速$\boxed{\text{2}}$より、かかる時間は$\boxed{{\displaystyle \frac{36}{2}}}$＝18分。

（答え）　18分

 

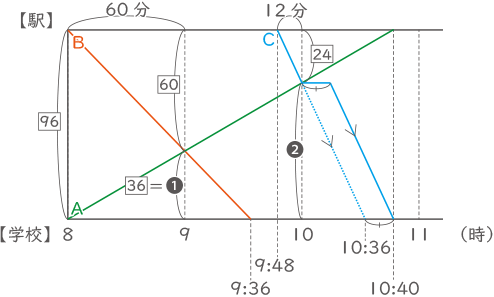
（3）
（1）と同様にBの分速を$\boxed{\text{1}}$とすると、駅学校間の距離は$\boxed{\text{96}}$と表せるので、$\boxed{\text{96}}$÷$\boxed{\text{1}}$＝96分。よって、9時36分。

（答え）　9時36分

 

（4）
Bの速さを同じく分速を$\boxed{\text{1}}$とすると、Aの速さは分速$\boxed{{\displaystyle \frac{36}{60}}}$＝$\boxed{{\displaystyle \frac{3}{5}}}$となり、距離$\boxed{\text{96}}$をAが歩く時間は$\boxed{\text{96}}$÷$\boxed{{\displaystyle \frac{3}{5}}}$＝160分で、10：40に駅に着く。
Cが休みなく歩くと、学校までかかる時間は、$\boxed{\text{96}}$÷$\boxed{\text{2}}$＝48分で、10：36に学校に着く。
10：40－10：36より、休んだ時間は4分となる。

（答え）　4分

 

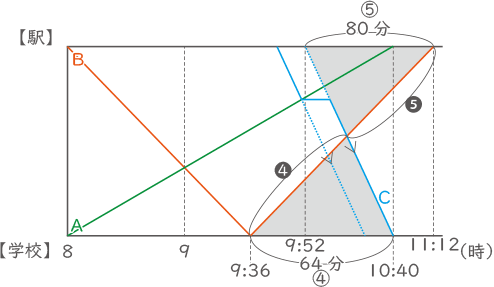
（5）
Cが休みなく歩いて10：40に学校に着くための出発時間は、10：40－48分より9：52。
Bは片道96分かかるので再び駅に着く時間は、8：00＋96×2より、11：12。
図の様に、❺：❹の相似な三角形を利用してBとCが出会う時間を求める。

9:36＋（11:12－9:36）×${\displaystyle \frac{❹}{❾}}$＝（9:36から42${\displaystyle \frac{2}{3}}$分後）＝10時18分40秒。

（答え）　10時18分40秒