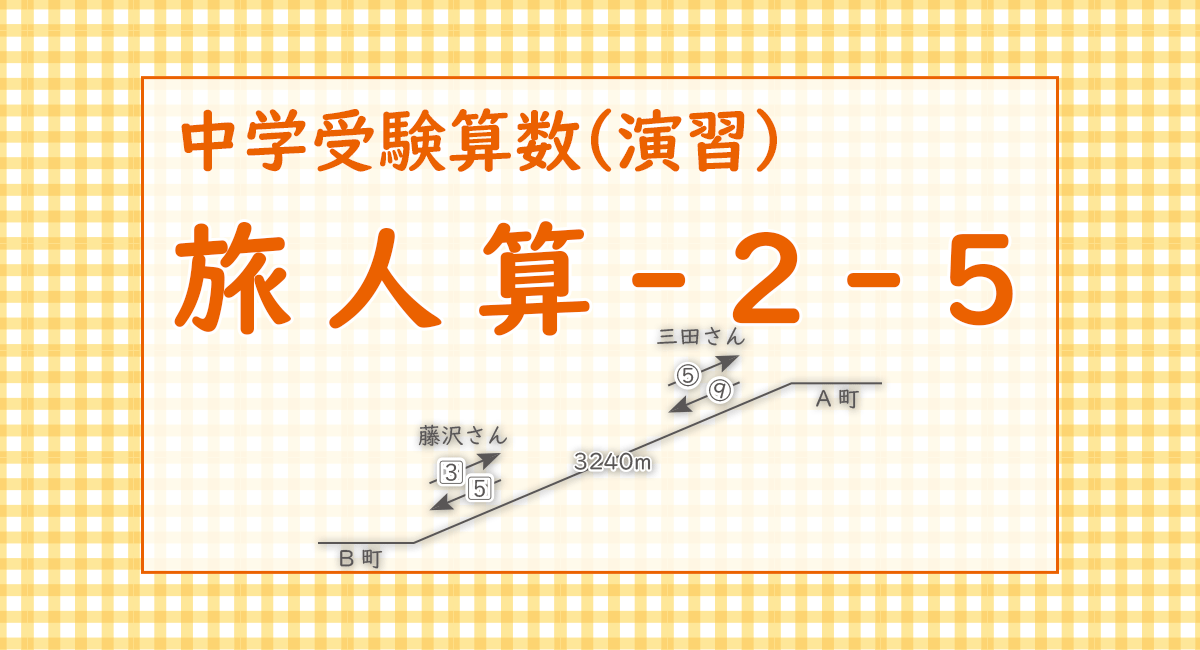
旅人算-2-5（慶應義塾湘南藤沢中等部2022/一問目ができればあとは簡単）

1 問題
2 解答

問題

問題（慶應義塾湘南藤沢中等部2022/一問目ができればあとは簡単）

山の頂上にA町が，山のふもとにB町があり，2つの町は3240mはなれている。三田さんはA町を，藤沢さんはB町を同時に出発して，A町とB町の間を一往復した。
三田さんの登る速さと下る速さの比は5：9
藤沢さんの登る速さと下る速さの比は3：5
であり，登りも下りも藤沢さんの方が三田さんより毎分6m速いという。

（1）三田さんの下る速さは分速何mですか。
（2） 2人が同時に出発して，最初に出会うのは何分後ですか。
（3） 2人が最初に出会ってから，2回目に出会うまでに何分かかりますか。

人里離れた旅館？それとも海辺のリゾートホテル？　中学受験の前に一区切り、受験前最後の家族旅行はお早めに。今がそのチャンスかも。

解答

解答を開く

（1）

問題文通りの式を作る。
⑤＋6m/分＝$ \fbox{3} $・・・❶
⑨＋6m/分＝$ \fbox{5} $・・・❷
❶×5、❷×3とし、
㉕＋30m/分＝$ \fbox{15} $
㉗＋18m/分＝$ \fbox{15} $
消去算で、
㉕＋30m/分＝㉗＋18m/分
②＝12m/分
三田さんの下る速さ⑨＝②×$ \displaystyle \frac{2}{9} $＝12×$ \displaystyle \frac{2}{9} $＝54、分速54m

（答え）　分速54m

（2）
三田さんの下る速さ⑨は54m/分
三田さんの登る速さ⑤＝②×$ \displaystyle \frac{5}{2} $＝12×$ \displaystyle \frac{5}{2} $＝30m/分

藤沢さんの下る速さ$ \fbox{5} $＝⑨＋6m/分＝60m/分
藤沢さんの登る速さ$ \fbox{3} $＝⑤＋6m/分＝36m/分

求める時間は、
3240÷（54＋36）＝36分

（答え）　36分

（3）
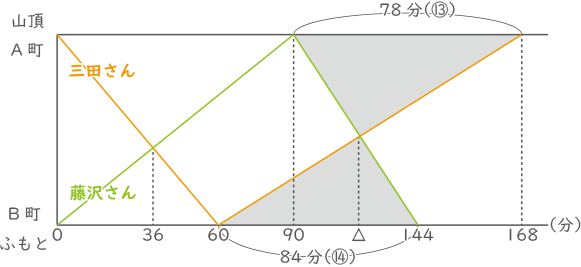
（2）で求めた２人の速さをもとにダイヤグラムをつくる。
【三田さんがかかる時間】
A町→B町：3240÷54＝60分
B町→A町：3240÷30＝108分
【藤沢さんがかかる時間】
A町→B町：3240÷60＝54分
B町→A町：3240÷36＝90分