問題
問題(学習院女子中等科2013/規則性はすぐ見つかるでの、あとは数えやすい形に整えればよい)
次のように規則的に整数が並んでいます。下の問いに答えなさい。
1,2,4,5,6,8,9,10,12,13,14,16,・・・
(1) 2013は何番目の整数ですか。
(2) はじめから100番目の整数は何ですか。
(3) はじめから100番目までの整数をたすといくつになりますか。
【家庭学習】過去問をA3で実サイズコピーして本番形式で臨みましょう
4.45
試験で使われる問題用紙はかなり大きめ。同じ大きさで過去問を用意して本番感覚を養いましょう。印刷するのはパパとママの役目。A3ノビまで対応、全色顔料インクで滲まない。最大給紙枚数は550枚。
解答
- 解答を開く
-
次のように規則的に整数が並んでいます。下の問いに答えなさい。
1,2,4,5,6,8,9,10,12,13,14,16,・・・(1) 2013は何番目の整数ですか。
(2) はじめから100番目の整数は何ですか。
(3) はじめから100番目までの整数をたすといくつになりますか。(1)
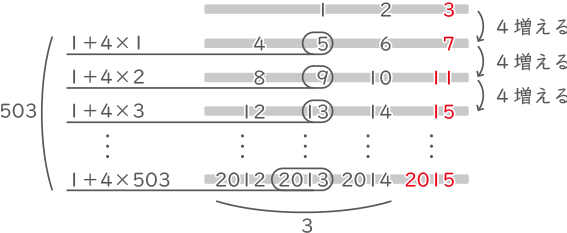
1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,・・・
規則性をもって数字が飛ばされているので、見やすい形に並べ替える。

503×3+2(1と2の分)-1(2014の分)=1510
(答え) 1510番目
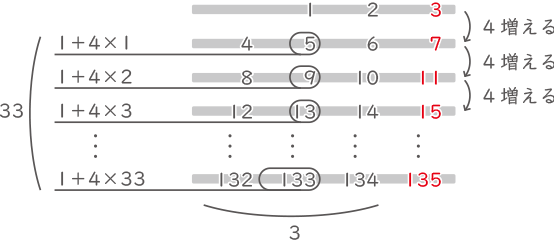
(2)

134が33×3+2=101番目の数なので、100番目の数は133
(答え) 133
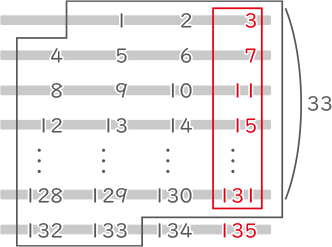
(2)

黒枠の数の和と赤枠の数の和の差を求める。
{(1+133)×133÷2}-{(3+131)×33÷2}=6700(答え) 6700
ではまた~