問題
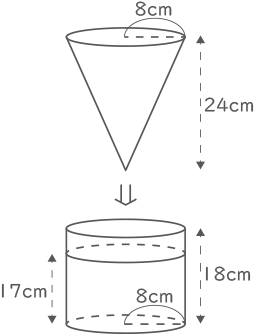 右の図のような,底面の半径8cm, 高さ18cmの円柱の容器に,高さ17cmのところまで水が入っています。
右の図のような,底面の半径8cm, 高さ18cmの円柱の容器に,高さ17cmのところまで水が入っています。
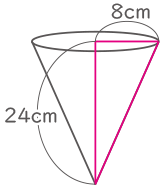
ここに,底面の半径8cm, 高さ24cmの円すいを,矢印の向きに沈(しず)めていきます。
円周率を3.14として,次の問に答えなさい。
(1) 水が容器からこぼれ始めるとき,円すいは水に何cm沈んでいますか。求め方と答えを書きなさい。
(2) 円すいの頂点を容器の底につけてから円すいを取り出すと,水の深さは□cmになります。
人里離れた旅館?それとも海辺のリゾートホテル? 中学受験の前に一区切り、受験前最後の家族旅行はお早めに。今がそのチャンスかも。
解答
- 解答を開く
-
 右の図のような,底面の半径8cm, 高さ18cmの円柱の容器に,高さ17cmのところまで水が入っています。
右の図のような,底面の半径8cm, 高さ18cmの円柱の容器に,高さ17cmのところまで水が入っています。
ここに,底面の半径8cm, 高さ24cmの円すいを,矢印の向きに沈(しず)めていきます。
円周率を3.14として,次の問に答えなさい。(1) 水が容器からこぼれ始めるとき,円すいは水に何cm沈んでいますか。求め方と答えを書きなさい。
(2) 円すいの頂点を容器の底につけてから円すいを取り出すと,水の深さは□cmになります。
(1)

三角すいの底面の半径と高さの比は8cm:24cm=1:3

水の量は(8×8×3.14×17)cm3
円柱の容積は(8×8×3.14×18)cm3
その差8×8×3.14×1=(64×3.14)cm3だけ三角すいが沈めば満水になる。
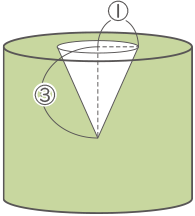
満水になった時の三角すいの水面の半径を①とすれば、水に沈んでいる深さ(高さ)は③となる。よって、
①×①×3.14×③×$ \displaystyle \frac{1}{3} $=①×①×①×3.14=64×3.14、
①=4、③=12cm(答え) 12cm
(2)

<(1)で求めた12cmよりも沈めるので水はあふれ出るとわかる>
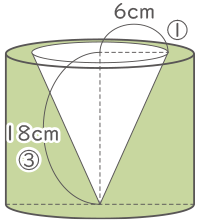
三角すいは18cmまで沈み、その時の水面の三角すいの半径は6cm
三角すいの沈んでいる部分の体積は(6×6×3.14×18×$ \displaystyle \frac{1}{3} $)cm3
円柱の容積は(8×8×3.14×18)cm3
三角すいを底まで沈めた時に残った水の量=円柱の容積-三角すいの沈んでいる部分の体積=8×8×3.14×18-(6×6×3.14×18×$ \displaystyle \frac{1}{3} $)=52×3.14×18
これを円柱の底面積で割れば残った水の高さがわかる。
52×3.14×18÷(8×8×3.14)=14.625(答え) 14.625cm