問題
3桁の数ABC,DEF,GHIの3つを足したら2022になりました。
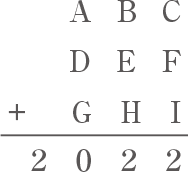
A~Iには,0~9の10個の数字のうち,9個の異なる数字が1つずつ入ります。また,Cは6,Hは0です。A~Iで使わなかった数字をPとします。
ABCが考えられる数の中で一番大きい数になるとき,BとPはそれぞれいくつですか。
Amazonブランドのタブレット[Fire HD 10 Plus タブレット10.1インチ]フルHDディスプレイ(1920×1200)だから広くて見やすく家勉の必需品。
解答
- 解答を開く
-
3桁の数ABC,DEF,GHIの3つを足したら2022になりました。

A~Iには,0~9の10個の数字のうち,9個の異なる数字が1つずつ入ります。また,Cは6,Hは0です。A~Iで使わなかった数字をPとします。
ABCが考えられる数の中で一番大きい数になるとき,BとPはそれぞれいくつですか。 (ⅰ)
(ⅰ)
FとIの和は6か16だが、問題条件より6に絞る。
FとIの候補は、
(1,5)・・・①
(2,4)・・・②(ⅱ)
一の位からの繰り上がりが1なので、BとEの和は11。
BとEの候補は、
(9,2)・・・③
(8,3)・・・④
(7,4)・・・⑤
(6,5)・・・×6は使えない(ⅲ)
十の位からの繰り上がりが1なのでAとDとGの和は19。
AとDとGの候補は、
(9,8,2)・・・⑥
(9,7,3)・・・⑦
(9,6,4)・・・×6は使えない
(8,7,4)・・・⑧
(8,6,5)・・・×6は使えない問題条件からAが一番大きくなる数を、次にBが大きくなる数を考える。
⑥と⑦両方とも9があるので最優先だが、⑦を使うと、十の位の③,④,⑤がどれも使われてしまうので外す。⑥で考えると、Aは9で、DとGは8と2のどちらか。9,8,2を使ったので十の位は⑤だけが使え、一の位は①だけが使える。
十の位に使える⑤より、Bは7で、Eが4。
一の位に使える①より、FとIは1と5のどちらか。
使わなかった数字Pは3となる。
(答え) Bは7,Pは3
この年、似たような問題がこの学校でも出題されています。
場合の数-3-1(市川中学2022/与えられた条件から9つの異なる数を見つけ出す)



 (ⅰ)
(ⅰ)