問題
【図1】のような,縦の長さ60cm,横の長さ90cm,深さ60cmの直方体の形をした浴槽(そう)に,1分間に18Lの水が出る蛇口(じゃぐち)から水を入れ始めました。水を入れ始めて12分経ったときに排水溝(はいすいこう)の栓(せん)を開けてしまい,6分後に栓が開いていることに気がつき栓を閉めました。水を入れ始めてから27分経ったときに満水になり,水を止めました。【図2】のグラフは,水を入れ始めてからの時間と水面の高さの関係を表したものです。このとき,次の各問いに答えなさい。ただし,浴槽の厚さは考えないものとします。
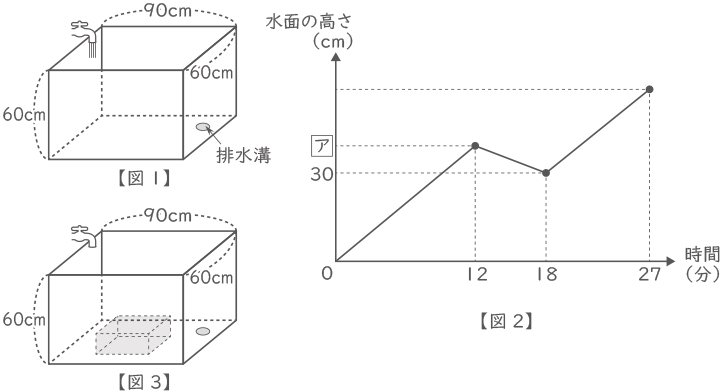
(1) グラフ中の$ \fbox{ア} $にあてはまる数を求めなさい。
(2) 排水溝から1分間に出る水の量を求めなさい。
(3) 満水になった浴槽に,【図3】のように,縦の長さ30cm,横の長さ50cm,高さ18cmの直方体の形のおもりを沈(しず)めると,水があふれました。その後,栓を抜(ぬ)いて水をすべて排水しました。排水し始めてから浴槽が空になるまでにかかった時間を求めなさい。
これまでほとんどの通信教育で実現できなかった難関国私立中学合格。Z会なら、可能です。【公立中高一貫校を受検予定 】の方は試しに資料請求してみましょう。HPにも「小学生コース専科 公立中高一貫校受検対策講座のご案内」が詳しく記載されています。
解答
- 解答を開く
-
【図1】のような,縦の長さ60cm,横の長さ90cm,深さ60cmの直方体の形をした浴槽(そう)に,1分間に18Lの水が出る蛇口(じゃぐち)から水を入れ始めました。水を入れ始めて12分経ったときに排水溝(はいすいこう)の栓(せん)を開けてしまい,6分後に栓が開いていることに気がつき栓を閉めました。水を入れ始めてから27分経ったときに満水になり,水を止めました。【図2】のグラフは,水を入れ始めてからの時間と水面の高さの関係を表したものです。このとき,次の各問いに答えなさい。ただし,浴槽の厚さは考えないものとします。

(1) グラフ中の$ \fbox{ア} $にあてはまる数を求めなさい。
(2) 排水溝から1分間に出る水の量を求めなさい。
(3) 満水になった浴槽に,【図3】のように,縦の長さ30cm,横の長さ50cm,高さ18cmの直方体の形のおもりを沈(しず)めると,水があふれました。その後,栓を抜(ぬ)いて水をすべて排水しました。排水し始めてから浴槽が空になるまでにかかった時間を求めなさい。(1)

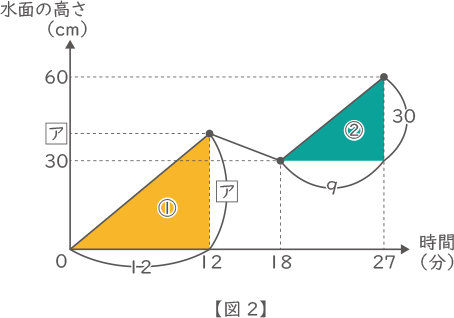
0分から12分までと18分から27分までの水面の上昇の割合は同じなので、①と②の三角形は相似となる。
9:30=3:10=12:$ \fbox{ア} $
$ \fbox{ア} $=40(答え) 40
(2)
排水溝を開けなかった場合の満水になるまでの時間は、(1)の②の三角形より、水位が30cm上がるのに9分かかるので、満水の60cm上がるまでには18分かかる。
途中で栓を開けたので満水になるまで9分(=27-18)多く時間がかかった。よって、9分間入れた水が、排水された水の量と等しい。
(1)の②の三角形より、9分間で水位が30cmが上がるので、その間に入った水量は、
90×60×30=162000cm3
栓が開いていた時間が6分間なので、1分当たり162000÷6=27000cm3(27L)出た。(答え) 27000cm3(27L)
(3)
満水時の水量:(90×60×60)cm3
おもりの容積:(30×50×18)cm3
1分当たりの排水量:27000cm3
おもりの入った浴槽の栓を開いて、空になるまでにかかった時間は、
{(90×60×60)-(30×50×18)}÷27000
={(90×60×60)-(30×2×5×5×18)}÷27000
={(90×60×60)-(60×5×90)}÷27000
=(90×60)×(60-5)÷27000
=(9×6)×(60-5)÷270
=54×55÷270
=27×2×55÷270
=27×11÷27
=11分(答え) 11分