問題
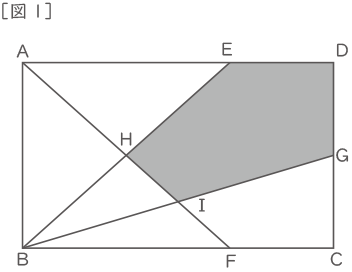
[図1]のような長方形ABCDがあります。辺AD、BCを2:1の比に分ける点をそれぞれE、Fとし、辺 CDを1:1の比に分ける点を Gとします。AFとBEの交わった点をHとし、AFとBGの交わった点をIとします。
このとき、BI:IG=(コ):(サ)になります。また、長方形ABCDの面積が180cm2のとき、色のついている部分の五角形DEHIGの面積は(シ)cm2になります。
ただし、(コ):(サ)は、もっとも簡単な整数の比で答えなさい。
これまでほとんどの通信教育で実現できなかった難関国私立中学合格。Z会なら、可能です。【公立中高一貫校を受検予定 】の方は試しに資料請求してみましょう。HPにも「小学生コース専科 公立中高一貫校受検対策講座のご案内」が詳しく記載されています。
解答
- 解答を開く
-
[図1]のような長方形ABCDがあります。辺AD、BCを2:1の比に分ける点をそれぞれE、Fとし、辺 CDを1:1の比に分ける点を Gとします。AFとBEの交わった点をHとし、AFとBGの交わった点をIとします。
このとき、BI:IG=(コ):(サ)になります。また、長方形ABCDの面積が180cm2のとき、色のついている部分の五角形DEHIGの面積は(シ)cm2になります。
ただし、(コ):(サ)は、もっとも簡単な整数の比で答えなさい。

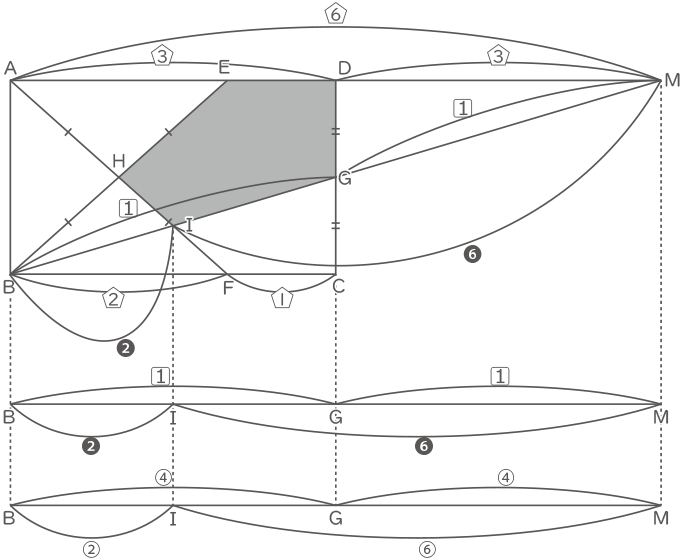
BG:GM=1:1、 BI:IM=2:6。
2種類の比の和、2と8の最小公倍数8にあわせた連比にすると、BI:IG:GM=②:(④-②):④=2:2:4=1:1:2
よって、BI:IG=1:1(答え) (コ):(サ)=1:1
比をふり直す。

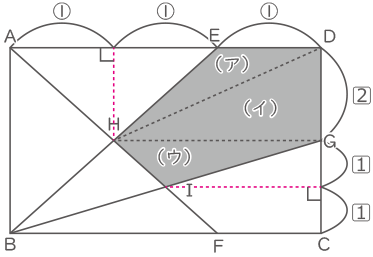
③×$ \fbox{4} $が180cm2になるので、①×3×$ \fbox{1} $×4=①×$ \fbox{1} $×12=180、
①×$ \fbox{1} $=15cm2となる。
(ア)=①×$ \fbox{2} $×$ \displaystyle \frac{1}{2} $=①×$ \fbox{1} $=15
(イ)=②×$ \fbox{2} $×$ \displaystyle \frac{1}{2} $=①×$ \fbox{1} $×2=30
(ウ)=②×$ \fbox{1} $×$ \displaystyle \frac{1}{2} $=①×$ \fbox{1} $=15
15+30+15=60cm2(答え) (シ) 60