問題
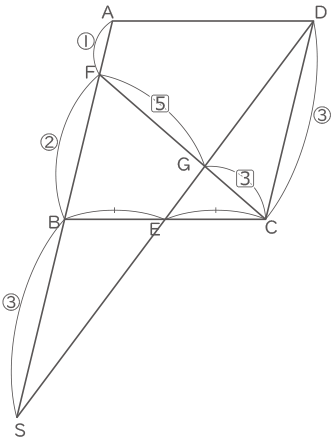
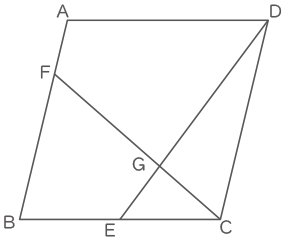
下の図の四角形ABCDは面積が60cm2の平行四辺形です。点Eは辺BCの中点です。また,AB上に点Fをとり,CFとDEの交点をGとすると,CG:GF=3:5となります。
次の問いに答えなさい。
(1) AF:FBの比を最も簡単な整数の比で表しなさい。
(2) 三角形FECの面積を求めなさい。
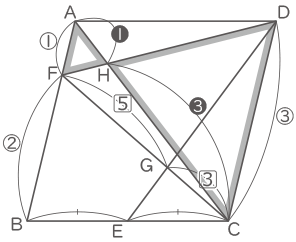
(3) ACとFDの交わる点をHとする。三角形AHFの面積を求めなさい。
教室には遠くて通えない、通塾負担を減らしたい。もしくは他の習い事が忙しくて、通塾の時間が取れない・・・ そんなご家庭に最適! 4大塾に通いながら弱点補強を家庭教師に任せているご家庭も多々、塾のクラスを上げるためにピンポイントでうまく利用しましょう。なにはともあれ資料請求してお子さんに合うか見てみましょう。
解答
- 解答を開く
-
下の図の四角形ABCDは面積が60cm2の平行四辺形です。点Eは辺BCの中点です。また,AB上に点Fをとり,CFとDEの交点をGとすると,CG:GF=3:5となります。
次の問いに答えなさい。
(1) AF:FBの比を最も簡単な整数の比で表しなさい。
(2) 三角形FECの面積を求めなさい。
(3) ACとFDの交わる点をHとする。三角形AHFの面積を求めなさい。
(1)
DEとABの延長線上の交点をSとおく。
三角形DCGと三角形SFGは相似より、CD:FS=③:⑤、よって、AF:FB=AF:(FS-BS)=①:(⑤-③)=①:②(答え) 1:2
(2)
四角形ABCDは面積が60cm2、
三角形ABCの面積はその半分の30cm2、
三角形FBCは高さが三角形ABCの$ \displaystyle \frac{2}{3} $なので20cm2、
三角形FECは三角形FBCの半分の長さの底辺なので10cm2。(答え) 10cm2

(3)

四角形ABCDは面積が60cm2、
三角形ABCの面積はその半分の30cm2、
三角形AFCは高さが三角形ABCの$ \displaystyle \frac{1}{3} $なので10cm2、
三角形AHFは三角形ACFの$ \displaystyle \frac{1}{4} $の長さの底辺なので$ \displaystyle \frac{10}{4} $=2.5cm2。(答え) 2.5cm2