問題
(1) 2桁の整数10,11,12, …,98,99について、7で割ったときの余りが1になる素数をすべて求めなさい。
(2) 7で割ると2余る2桁の整数と7で割ると3余る2桁の整数がある。この2つの数の合計が5の倍数になるとき, 2つの数の合計の中で2番目に小さい値を答えなさい。
(3) Aを7で割った余りがCで、Bを7で割った余りがDのとき,A×Bを7で割った余りはC×Dを7で割った余りに等しいことがわかっています。
10×10,11×11,12×12,…,98×98,99×99の整数について、7で割ったときの余りが1になる数の個数を求めなさい。
これまでほとんどの通信教育で実現できなかった難関国私立中学合格。Z会なら、可能です。【公立中高一貫校を受検予定 】の方は試しに資料請求してみましょう。HPにも「小学生コース専科 公立中高一貫校受検対策講座のご案内」が詳しく記載されています。
解答
- 解答を開く
-
(1) 2桁の整数10,11,12, …,98,99について、7で割ったときの余りが1になる素数をすべて求めなさい。
(2) 7で割ると2余る2桁の整数と7で割ると3余る2桁の整数がある。この2つの数の合計が5の倍数になるとき, 2つの数の合計の中で2番目に小さい値を答えなさい。
(3) Aを7で割った余りがCで、Bを7で割った余りがDのとき,A×Bを7で割った余りはC×Dを7で割った余りに等しいことがわかっています。
10×10,11×11,12×12,…,98×98,99×99の整数について、7で割ったときの余りが1になる数の個数を求めなさい。 (1)
(1)
図の様に並べてみると条件に当てはまるのは、29,43,71の3つ。(答え) 29,43,71
 (2)
(2)
図の様に並べてみると条件に当てはまるのは、37+38=75。(答え) 75
(3)
問題文の通りに表にしたものが下記。
7で割ったときの余りが1になる数の個数は13+13=26個。
(答え) 26個


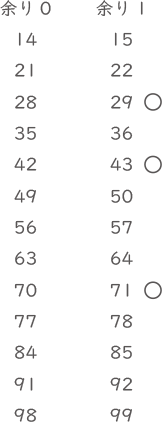 (1)
(1)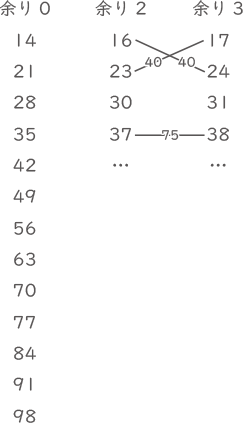 (2)
(2)