仕事算-2-4（女子学院中学2022/最後の問題で計算時間を取られるが完答者は多そう）

問題

解答

 解答を開く

 

次の□にあてはまる数を入れなさい。

A，B，Cの3台の機械は，それぞれ常に一定の速さで作業をします。BとCの作業の速さの比は5：4です。

ある日，A，B，Cで別々に，それぞれ同じ量の作業をしました。3台同時に作業を始め，Bが$ \displaystyle \frac{1}{4} $を終えた6分後にAが$ \displaystyle \frac{1}{4} $を終えて，Aが$ \displaystyle \frac{2}{3} $を終えた12分後にCが$ \displaystyle \frac{2}{3} $を終えました。
作業にかかった時間は，Aが□時間□分，Bが□時間□分でした。

次の日，前日に3台で行ったすべての量の作業をA，Bの2台でしました。
2台同時に作業を始めてから，□時間□分□秒ですべての作業が終わりました。

 

---

 

Bが$ \displaystyle \frac{1}{4} $を終えた6分後にAが$ \displaystyle \frac{1}{4} $を終えた
↓
Bが$ \displaystyle \frac{1}{4} $×4（作業全体）を終えた（6×4）分後にAが$ \displaystyle \frac{1}{4} $×4（作業全体）を終えた

Aが$ \displaystyle \frac{2}{3} $を終えた12分後にCが$ \displaystyle \frac{2}{3} $を終えた
↓
Aが$ \displaystyle \frac{2}{3} $×$ \displaystyle \frac{3}{2} $（作業全体）を終えた（12×$ \displaystyle \frac{3}{2} $）分後にCが$ \displaystyle \frac{2}{3} $×$ \displaystyle \frac{3}{2} $（作業全体）を終えた

つまり、Aが作業を終えた時、Bは作業を終えて24分経ち、Cはあと18分で作業が終わる。また、BとCの作業にかかる時間は速さの逆比で④：⑤となる。
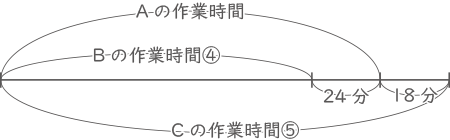
これを線分図で表す。

（この線分図が出来たらもう解けたも同然）
①が24＋18＝42分なので、④＝168分、⑤＝210分。
Aの作業時間＝168＋24＝192分＝3時間12分・・・（1つめの答え）
Bの作業時間＝168分＝2時間48分・・・（２つ目の答え）

 

前日に1台で行った作業量を$ \fbox{1} $とすると全ての作業量は$ \fbox{3} $。
Aの1分当たりの作業量は$ \fbox{\( \displaystyle \frac{1}{192} \)} $
Bの1分当たりの作業量は$ \fbox{\( \displaystyle \frac{1}{168} \)} $
合わせた1分当たりの作業量は$ \fbox{\( \displaystyle \frac{1}{192} \)} $＋$ \fbox{\( \displaystyle \frac{1}{168} \)} $＝$ \fbox{\( \displaystyle \frac{7}{192×7} \)} $＋$ \fbox{\( \displaystyle \frac{8}{168×8} \)} $
＝$ \fbox{\( \displaystyle \frac{5}{2×4×7×8} \)} $＝$ \fbox{\( \displaystyle \frac{5}{448} \)} $

よって作業量$ \fbox{3} $をこなす時間は$ \fbox{3} $÷$ \fbox{\( \displaystyle \frac{5}{448} \)} $＝268.8分＝4時間28分48秒。

（答え）　A，3時間12分　B，2時間48分　2台同時，4時間28分48秒