問題
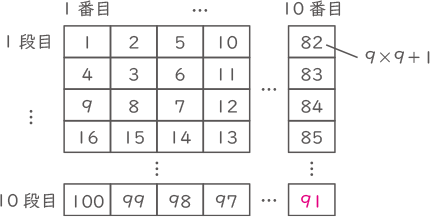
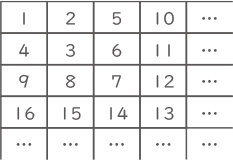右の図のように整数を1から順に並べていくことにします。17以降もこの規則で並べていきます。このとき、次の問いに答えなさい。
（1） 上から8段目、左から1番目の整数はいくつですか。
（2） 左上から右下にかけて並ぶ数1、3、7、13、……を考えたとき10番目の整数はいくつですか。
（3） 2022は上から何段目、左から何番目の位置にありますか。
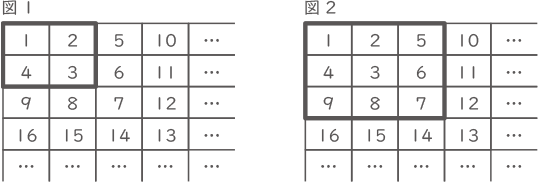
（4 ）図1のように左上の整数を1として□（太枠）を作り、□（太枠）内にあるすべての整数をたしたものを、【横2行、たて2列目の和】とします。同様にして、図2の場合、【横3行、たて3列目の和】となります。このとき、【横［ア］行、たて［ア］列目の和】が3321になるとき、［ア］ にあてはまる数はいくつですか。途中の考え方や式も書きなさい。ただし、［ア］ には同じ数が入ります。
Amazonブランドのタブレット［Fire HD 10 Plus タブレット10.1インチ］フルHDディスプレイ(1920×1200)だから広くて見やすく家勉の必需品。
解答
- 解答を開く
-
右の図のように整数を1から順に並べていくことにします。17以降もこの規則で並べていきます。このとき、次の問いに答えなさい。（1） 上から8段目、左から1番目の整数はいくつですか。
（2） 左上から右下にかけて並ぶ数1、3、7、13、……を考えたとき10番目の整数はいくつですか。
（3） 2022は上から何段目、左から何番目の位置にありますか。
（4 ）図1のように左上の整数を1として□（太枠）を作り、□（太枠）内にあるすべての整数をたしたものを、【横2行、たて2列目の和】とします。同様にして、図2の場合、【横3行、たて3列目の和】となります。このとき、【横［ア］行、たて［ア］列目の和】が3321になるとき、［ア］ にあてはまる数はいくつですか。途中の考え方や式も書きなさい。ただし、［ア］ には同じ数が入ります。
（1）
左から1番目の数は全て平方数となっているので、上から8段目の数は8×8＝64（答え） 64
（2）
左から1番目の数で、上から10段目の数は10×10＝100なので、9個戻って91。
（答え） 91
（3）
45×45＝2025なので2022は上から45段目にある。また、2025が左から1番目にあるので3つ戻った左から4番目に2022はある。（答え） 上から45段目、左から4番目
（4）
【横2行、たて2列目の和】
1＋2＋3＋4＝（1＋4）×4×$ \displaystyle \frac{1}{2} $＝10【横3行、たて3列目の和】
1＋2＋3＋4＋５＋６＋７＋８＋９＝（1＋9）×9×$ \displaystyle \frac{1}{2} $＝45【横［ア］行、たて［ア］列目の和】
上からア段目の数を□とする。
1＋2＋3・・・＋□＝（1＋□）×□×$ \displaystyle \frac{1}{2} $＝3321
（1＋□）×□＝6642
□の検討をつけるにあたり、80×80＝6400はすぐに思いつくので１ずつ数をずらしてゆく。
81×80＝6480・・・×
82×81＝6442・・・〇
□は81とわかるので［ア］は9となる。（答え） 9
