問題
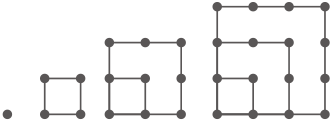 ある数のご石が右の図のような正方形の形に並べられるときに,その数を四角数(しかくすう)といいます。はじめの4つの四角数は,1,4,9,16です。10番目の四角数は[ ア ]です。[ イ ]番目の四角数は576です。
ある数のご石が右の図のような正方形の形に並べられるときに,その数を四角数(しかくすう)といいます。はじめの4つの四角数は,1,4,9,16です。10番目の四角数は[ ア ]です。[ イ ]番目の四角数は576です。
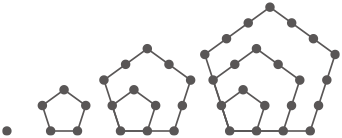 また,ある数のご石が右の図のような正五角形の形に並べられるときに,その数を五角数(ごかくすう)といいます。はじめの4つの五角数は,1,5, 12, 22です。10番目の五角数は[ ウ ]です。[ エ ]番目の五角数は425です。
また,ある数のご石が右の図のような正五角形の形に並べられるときに,その数を五角数(ごかくすう)といいます。はじめの4つの五角数は,1,5, 12, 22です。10番目の五角数は[ ウ ]です。[ エ ]番目の五角数は425です。
試験で使われる問題用紙はかなり大きめ。同じ大きさで過去問を用意して本番感覚を養いましょう。印刷するのはパパとママの役目。A3ノビまで対応、全色顔料インクで滲まない。最大給紙枚数は550枚。
解答
- 解答を開く
-
 ある数のご石が右の図のような正方形の形に並べられるときに,その数を四角数(しかくすう)といいます。はじめの4つの四角数は,1,4,9,16です。10番目の四角数は[ ア ]です。[ イ ]番目の四角数は576です。
ある数のご石が右の図のような正方形の形に並べられるときに,その数を四角数(しかくすう)といいます。はじめの4つの四角数は,1,4,9,16です。10番目の四角数は[ ア ]です。[ イ ]番目の四角数は576です。 また,ある数のご石が右の図のような正五角形の形に並べられるときに,その数を五角数(ごかくすう)といいます。はじめの4つの五角数は,1,5, 12, 22です。10番目の五角数は[ ウ ]です。[ エ ]番目の五角数は425です。
また,ある数のご石が右の図のような正五角形の形に並べられるときに,その数を五角数(ごかくすう)といいます。はじめの4つの五角数は,1,5, 12, 22です。10番目の五角数は[ ウ ]です。[ エ ]番目の五角数は425です。[ ア ]
集まった点の形を正方形としてとらえると、10番目の四角数は10×10=100。(答え) 100
[ イ ]
576=□×□となる□をもとめるために素因数分解する。
576=2×2×2×2×2×2×3×3=(2×2×2×3)×(2×2×2×3)=24×24
よって、576は24番目の四角数。(答え) 24
[ ウ ]
(数の規則性を調べる。)
1番目の五角数は1
2番目の五角数は5=1+4
3番目の五角数は12=1+4+7
4番目の五角数は22=1+4+7+10
・・・
10番目の五角数は1+4+7+…+㋒=㋑
よって、㋒がわかれば10番目の五角数㋑もわかる。
4、7、10は3ずつ増えているので9コ目の数㋒は、4、7、10、13、16、19、22、25、28より28とわかり、10番目の五角数は1+4+7+…+28=(1+28)×10×$ \displaystyle \frac{1}{2} $=145(答え) 145
[ エ ]
[ ウ ]で考えた3ずつ増えている9コ目の数㋒が28なので、28、31、34、37、40、43、46、49、52、55、…として13コ目の数40で試してみる。
(前問の答えが125、今回は425なので近い数で試す。
前問の10番目の五角数の式、(1+28)×10×$ \displaystyle \frac{1}{2} $=145を利用する。)
13コ目の数40を使うと、14番目の五角数は1+4+7+…+40=(1+40)×14×$ \displaystyle \frac{1}{2} $=287となり足りない。
14コ目の数43を使うと、15番目の五角数は1+4+7+…+43=(1+43)×15×$ \displaystyle \frac{1}{2} $=330となり足りない。少し飛ばした数にする。
16コ目の数49を使うと、17番目の五角数は1+4+7+…+49=(1+49)×17×$ \displaystyle \frac{1}{2} $=425となり数が合った。(答え) 17
補足([ ウ ]・[ エ ]の別解)1番目の五角数は1=(1×1)+0
2番目の五角数は5=(2×2)+1
3番目の五角数は12=(3×3)+1+2
4番目の五角数は22=(4×4)+1+2+3
5番目の五角数は35=(5×5)+1+2+3+4
6番目の五角数は51=(6×6)+1+2+3+4+5
・・・
10番目の五角数は145=(10×10)+1+2+3+・・・+9・・・[ ウ ]
・・・
16番目の五角数は376=(16×16)+1+2+3+・・・+15
17番目の五角数は425=(17×17)+1+2+3+・・・+16・・・[ エ ]
青字が四角数、赤字が三角数になっている。