問題
消しゴムと鉛筆を生徒に配りました。消しゴムは3個ずつ、消しゴムの数の4倍ある鉛筆は14本ずつ配ると、消しゴムは7個余り、鉛筆はちょうど無くなりました。このことより、消しゴムは(①)個、鉛筆は(②)本、生徒は(③)人です。
これまでほとんどの通信教育で実現できなかった難関国私立中学合格。Z会なら、可能です。【公立中高一貫校を受検予定 】の方は試しに資料請求してみましょう。HPにも「小学生コース専科 公立中高一貫校受検対策講座のご案内」が詳しく記載されています。
解答
- 解答を開く
-
消しゴムと鉛筆を生徒に配りました。消しゴムは3個ずつ、消しゴムの数の4倍ある鉛筆は14本ずつ配ると、消しゴムは7個余り、鉛筆はちょうど無くなりました。このことより、消しゴムは(①)個、鉛筆は(②)本、生徒は(③)人です。
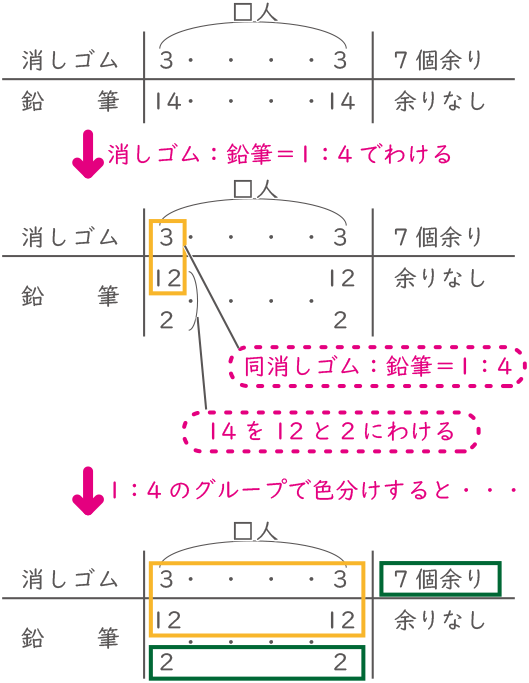
まずは図表を書いてイメージをつかむ。さらに、消しゴム:鉛筆=1:4も図表内で利用する。

黄色枠は、消しゴム:鉛筆=1:4にわけられたので、緑枠も同様に1:4になる。余りの消しゴムが7個あるので、下側の緑枠にはその4倍の28本の鉛筆があるとわかる。よって□=28÷2=14(生徒数)。
消しゴム=3×14+7=49個、鉛筆=14×14=196本となる。(答え)①49 ②196 ③14
- 別解を開く
-
消しゴムと鉛筆を生徒に配りました。消しゴムは3個ずつ、消しゴムの数の4倍ある鉛筆は14本ずつ配ると、消しゴムは7個余り、鉛筆はちょうど無くなりました。このことより、消しゴムは(①)個、鉛筆は(②)本、生徒は(③)人です。
消去算・代入法がわかるのであれば簡単。
生徒数を□とすると、消しゴムは3×□+7、鉛筆は14×□となり、鉛筆は消しゴムの4倍なので、
消しゴム:3×□+7=①
鉛筆:14×□=④消しゴムの式を4倍にすると、
消しゴム×4:12×□+28=④
鉛筆:14×□=④よって、
12×□+28=14×□となり、
12×□+28=12×□+2×□
28=2×□
□=14
よって、生徒数14人となり、
消しゴム=3×14+7=49個、
鉛筆=14×14=196本となる。(答え)①49 ②196 ③14