
問題
下の図のような,1周が350mのプールがあリます。このプールには図の矢印方向に毎分60mの速さで水が流れています。このプールでおもちゃのボートを動かします。
静水時に毎分90mの速さで進むおもちゃのボートA,B,Cを用意しました。
(注意:この問題は,解き方を式や言葉などを使って書きなさい。)
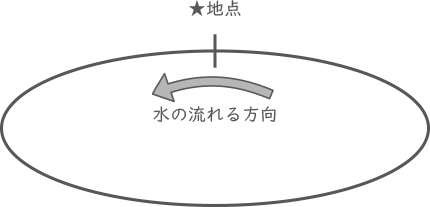
(1) ボートAがプールの水の流れと逆の方向に進むとき,プールを1周するのに何分何秒かかリますか。
(2) ボートAは水の流れと逆の方向に,ボートBは水の流れと同じ方向に,同時に★地点から動かし始めます。このとき,ボートAとボートBが初めて出会うのは,★地点からボートBが何m進んだ地点ですか。
(3) 上の(2)と同じようにボートBを動かし始めた後,★地点に同じおもちゃのボートCを浮かべて水の流れだけで進ませます。ボートBがボートCに2回目に追いつく場所が(2)で求めた地点と同じ地点となるようにするとき,ボートCはボートBが動き始めてから何分何秒後に浮かべればよいですか。
ただし,ボートBがプールを1周する前に,ボートCを★地点に浮かべます。
Amazonブランドのタブレット[Fire HD 10 Plus タブレット10.1インチ]フルHDディスプレイ(1920×1200)だから広くて見やすく家勉の必需品。
解答
- 解答を開く
-
下の図のような,1周が350mのプールがあリます。このプールには図の矢印方向に毎分60mの速さで水が流れています。このプールでおもちゃのボートを動かします。
静水時に毎分90mの速さで進むおもちゃのボートA,B,Cを用意しました。
(注意:この問題は,解き方を式や言葉などを使って書きなさい。)
(1) ボートAがプールの水の流れと逆の方向に進むとき,プールを1周するのに何分何秒かかリますか。
(2) ボートAは水の流れと逆の方向に,ボートBは水の流れと同じ方向に,同時に★地点から動かし始めます。このとき,ボートAとボートBが初めて出会うのは,★地点からボートBが何m進んだ地点ですか。
(3) 上の(2)と同じようにボートBを動かし始めた後,★地点に同じおもちゃのボートCを浮かべて水の流れだけで進ませます。ボートBがボートCに2回目に追いつく場所が(2)で求めた地点と同じ地点となるようにするとき,ボートCはボートBが動き始めてから何分何秒後に浮かべればよいですか。
ただし,ボートBがプールを1周する前に,ボートCを★地点に浮かべます。(1)
350÷(90-60)=11$ \displaystyle \frac{2}{3} $=11$ \displaystyle \frac{40}{60} $=11分40秒(答え) 11分40秒
(2)
2つのボートが出会う時間は水の流れによらないので、
350÷(90+90)=$ \displaystyle \frac{35}{18} $分
★地点からボートBが進んだ距離=(90+60)×$ \displaystyle \frac{35}{18} $=291$ \displaystyle \frac{2}{3} $m(答え) 291$ \displaystyle \frac{2}{3} $m
(3)
BとCが同時に★地点を動き始めた場合を考える【Cが(2)で求めた地点に着く時間】
291$ \displaystyle \frac{2}{3} $÷60=4$ \displaystyle \frac{31}{36} $分【Bが(2)で求めた地点に初めて着く時間】
291$ \displaystyle \frac{2}{3} $÷150=1$ \displaystyle \frac{17}{18} $分【Bが(2)で求めた地点に2回目に着く時間】
(291$ \displaystyle \frac{2}{3} $+350)÷150=4$ \displaystyle \frac{5}{18} $分
このとき、BはCを1回追いこしている【Bが(2)で求めた地点に3回目に着く時間】
(291$ \displaystyle \frac{2}{3} $+350×2)÷150=6$ \displaystyle \frac{11}{18} $分
このとき、BはCに2回目に追い付く地点より手前にいる以上のことより、
6$ \displaystyle \frac{11}{18} $分-4$ \displaystyle \frac{31}{36} $分=1$ \displaystyle \frac{45}{60} $分、1分45秒遅くCを浮かべれば、BとCが同時に(2)で求めた地点に着く。
(答え) 1分45秒後












