流水算-2-3（桜蔭中学2022/ダイヤグラムから相似な三角形を作ると計算が簡単になる）

問題

解答

 解答を開く

 

一定の速さで流れている川の上流に地点A があり，その5km 下流に地点C があります。
2地点A，Cの間に地点Bがあり，AB間の距離はBC間の距離よりも短いです。
2せきの定期船P，Qは，
PはA→B→C→B→A→……,QはC→B→A→B→C→……
の順でAC間を往復します。
PはAから，QはCから同時に出発し，出発した後の地点A，B，Cではそれぞれ5分とまります。
2せきの船の静水時の速さは同じであリ，川の流れの速さの4倍です。
船がAを出発してから，はじめてCに着くまでに25分かかります。
ただし，川の幅は考えないこととします。

（1） 静水時の船の速さは分速何mですか。
（2） P，Qは，2地点B,Cの間で初めて出会いました。その地点をDとするとき，AD間の距離は何mですか。
（3） P，Qが2回目に出会ったのは地点Bでした。このとき，PはちょうどBを出発するところで，QはちょうどBに着いたところでした。AB間の距離は何mですか。

 

---

 

（1）
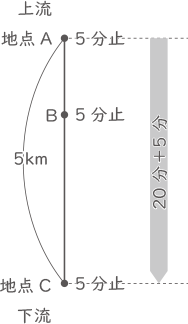
船の静水時の速さ：川の流れの速さ＝④：①。
地点Aから出発した船は地点Bでの5分間の停止が無ければ20分で地点Cに着く。
下りの船の速さは⑤（＝④＋①）。
5000(m)÷⑤＝20（分）、①＝50m/分
よって、
静水時の船の速さ④＝200m/分・・・（答え）
川の流れの速さ①＝50m/分
下りの船の速さ④＋①＝250m/分
上りの船の速さ④－①＝150m/分

 

 

（答え）　分速200m

 

（2）
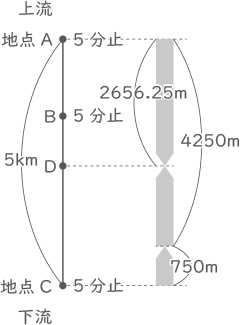
地点Bで5分停止するので、地点Aからの出発が地点Cからの出発より5分遅いものとして計算する。
下りの船が5分間に進む距離＝150×5＝750m、
上りの船が出発してから下りの船に出会うまでの時間＝（5000－750）÷（250＋150）＝$ \displaystyle \frac{85}{8} $分、
AD間の距離＝250×$ \displaystyle \frac{85}{8} $＝2656.25m

（答え）　2656.25m

 

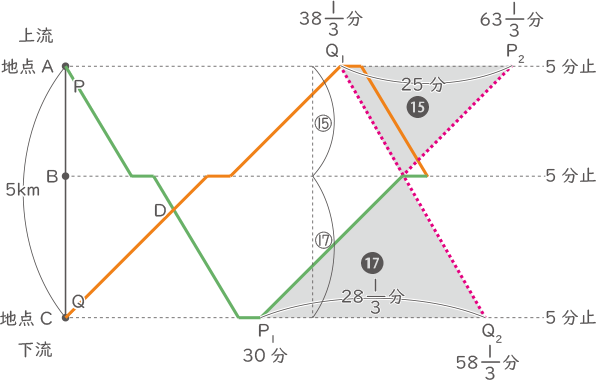
（3）
5kmを上る時間：5000÷150＝33$ \displaystyle \frac{1}{3} $分
5kmを下る時間：5000÷250＝20分
Q₁：33$ \displaystyle \frac{1}{3} $＋5＝38$ \displaystyle \frac{1}{3} $分
Q₂：38$ \displaystyle \frac{1}{3} $＋20＝58$ \displaystyle \frac{1}{3} $分
P₁：20＋10＝30分
P₂：30＋33$ \displaystyle \frac{1}{3} $＝63$ \displaystyle \frac{1}{3} $分

2つの灰色の三角形は相似なので、
P₂Q₁＝63$ \displaystyle \frac{1}{3} $分－38$ \displaystyle \frac{1}{3} $分=25分
Q₂P₁＝58$ \displaystyle \frac{1}{3} $分－30分=28$ \displaystyle \frac{1}{3} $分
P₂Q₁：Q₂P₁＝25：28$ \displaystyle \frac{1}{3} $＝⓯：⓲
AB間の距離＝5000×$ \displaystyle \frac{⑮}{⑮+⑰} $＝2343.75m

（答え）　2343.75m