問題
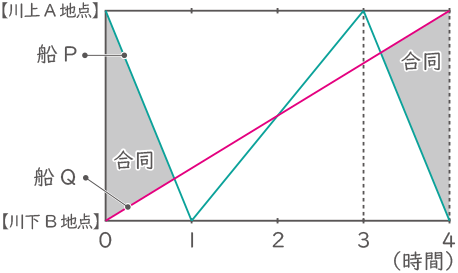
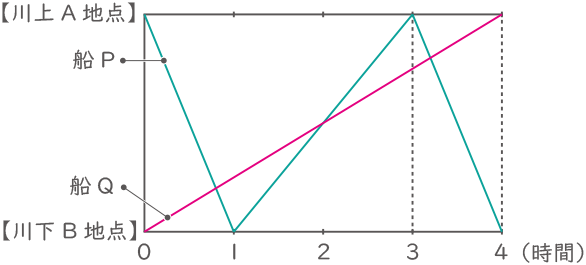
川上のA地点と川下のB地点を往復する2せきの船Pと船Qの様子をグラフに表しました。P、Qの船は同時に出発し、反対側に到着後すぐに折り返します。川の流れの速さは時速3.2kmです。
(1) 船Pと船Qが2回目に出会うのは同時に出発してから何時間何分後ですか。
(2) 船Qの下りの速さは時速何kmですか。
教室には遠くて通えない、通塾負担を減らしたい。もしくは他の習い事が忙しくて、通塾の時間が取れない・・・ そんなご家庭に最適! 4大塾に通いながら弱点補強を家庭教師に任せているご家庭も多々、塾のクラスを上げるためにピンポイントでうまく利用しましょう。なにはともあれ資料請求してお子さんに合うか見てみましょう。
解答
- 解答を開く
-
川上のA地点と川下のB地点を往復する2せきの船Pと船Qの様子をグラフに表しました。P、Qの船は同時に出発し、反対側に到着後すぐに折り返します。川の流れの速さは時速3.2kmです。
(1) 船Pと船Qが2回目に出会うのは同時に出発してから何時間何分後ですか。
(2) 船Qの下りの速さは時速何kmですか。

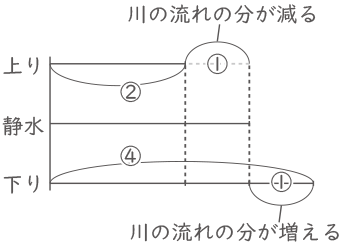
(1)船Pは下りが1時間、上りが2時間かかるので速さは逆比より、下り:上り=2:1(=④:②)となる。
川の流れの速さは(④-②)÷2=①で、①は時速3.2kmなので、船Pの下りの速さは④=3.2×4で時速12.8km。
また、AB地点間は時速12.8km×1時間=12.8km。船Qの上りの速さは12.8÷4=時速3.2km。
1回目と2回目に出会うグラフに合同な三角形があるので、(2回目に出会う時間)=(4時間後)-(1回目に出会う時間)で求められる。
1回目に出会う時間=12.8÷(12.8+3.2)=0.8、よって2回目に出会う時間=4-0.8=3.2時間=3時間12分後。
(答え)3時間12分後
(2)船Qの下りの速さ
=船Qの上りの速さ+川の流れの速さ×2
=3.2+3.2×2=9.6、時速9.6kmとなる。(答え)時速9.6km