問題
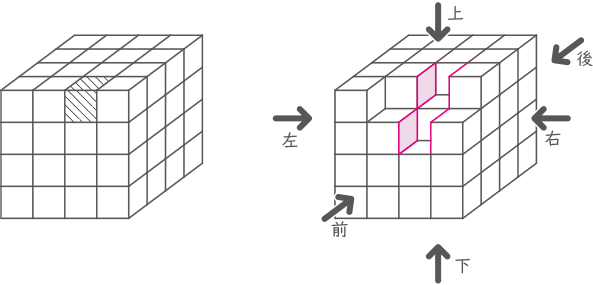
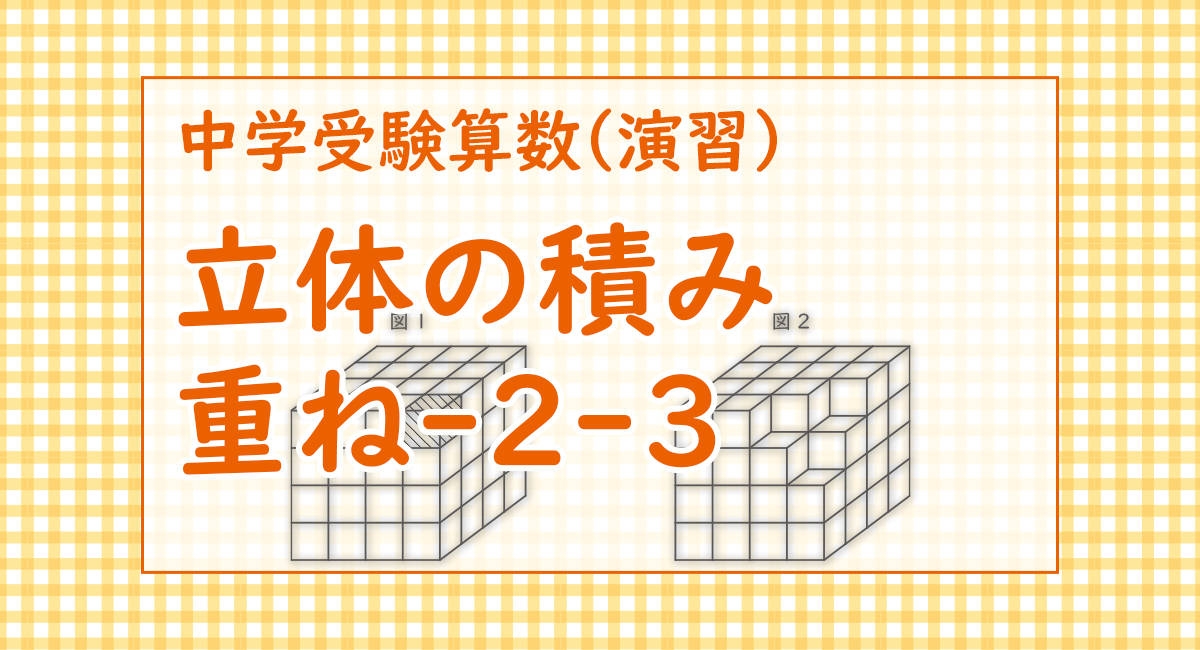
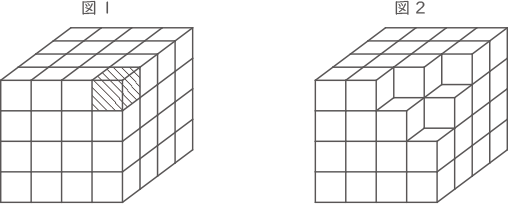
1辺の長さが1cmの立方体を64個積み重ねて,1辺の長さが4cmの立方体を作ります。色がぬられた立方体がある場合は,色がぬられた立方体と,それととなり合う立方体を取り除きます。例えば,図1のように色がぬられた立方体が1つあるときは,図2のように4つの立方体を取り除いた立体ができます。
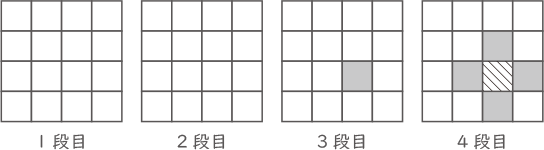
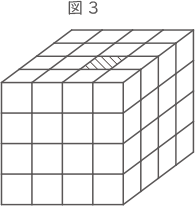 (1) 図3のように色がぬられた立方体が1つあるとき,できた立体の体積は何cm3ですか。
(1) 図3のように色がぬられた立方体が1つあるとき,できた立体の体積は何cm3ですか。
(2) 1番上の段に色がぬられた立方体が1つあるとき,できた立体の表面積は100cm2でした。色がぬられた立方体の位置として考えられるものは何通りありますか。
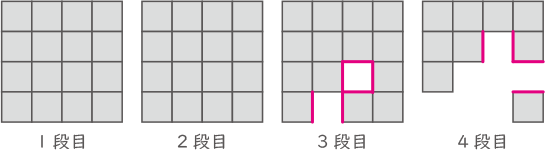
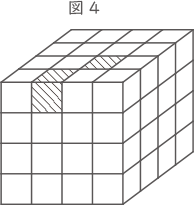 (3) 図4のように色がぬられた立方体が2つあるとき,できた立体の表面積は何cm2ですか。
(3) 図4のように色がぬられた立方体が2つあるとき,できた立体の表面積は何cm2ですか。
四谷大塚の対面授業の指導力と、東進の映像制作技術を融合した東進オンライン学校。わかりやすくて面白いから、楽しみながら勉強が続けられます。 <オンラインなので全国どこからでも自宅で超一流の先生の授業を受けられます!しかも授業料は【格安】>
解答
- 解答を開く
-
1辺の長さが1cmの立方体を64個積み重ねて,1辺の長さが4cmの立方体を作ります。色がぬられた立方体がある場合は,色がぬられた立方体と,それととなり合う立方体を取り除きます。例えば,図1のように色がぬられた立方体が1つあるときは,図2のように4つの立方体を取り除いた立体ができます。

 (1) 図3のように色がぬられた立方体が1つあるとき,できた立体の体積は何cm3ですか。
(1) 図3のように色がぬられた立方体が1つあるとき,できた立体の体積は何cm3ですか。(2) 1番上の段に色がぬられた立方体が1つあるとき,できた立体の表面積は100cm2でした。色がぬられた立方体の位置として考えられるものは何通りありますか。
 (3) 図4のように色がぬられた立方体が2つあるとき,できた立体の表面積は何cm2ですか。
(3) 図4のように色がぬられた立方体が2つあるとき,できた立体の表面積は何cm2ですか。(1)
各段を上から見る。
残った立方体は58個で体積は58cm3
(答え) 58cm3
(2)
全ての立方体がある場合の表面積は96cm2、それに対して100cm2であれば立方体の面が4面分多い状態 ⇒ 上下左右前後から見て隠れる面が4つある形になればよい
(隠れる面が無ければ一部の立体が取り除かれていても表面積は変わらない。)
上の図と同じようになるのは8通り。
(答え) 8通り
(3)
図形を上下左右前後から見ると面に欠けが無いので表面積は96cm2以上とわかる。
よって、上下左右前後からみた際に隠れる面を数えればよい。図の様に、各段を上から見た場合を考えると、隠れる面は赤線のところになる。
隠れる面は10カ所
よって、96+10=106cm2
(答え) 106cm2