問題
問題（法政大学中学2020/積み重ねた立方体を真正面と真上から見る）
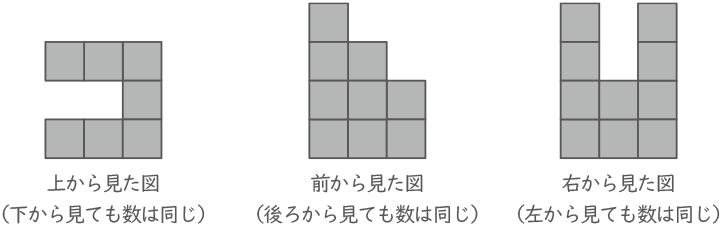
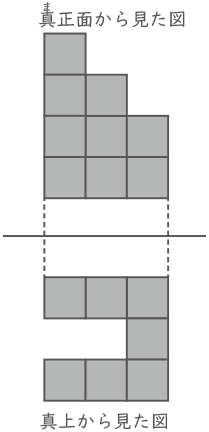1辺が1cmの立方体をすきまなく積み重ねて，右の図のような立体をつくりました。次の問いに答えなさい。
（1） 立方体の数は何個以上何個以下といえますか。
（2） 立方体の数がもっとも多い個数となるとき，この立体の表面積を求めなさい。
【家庭学習】過去問をA３で実サイズコピーして本番形式で臨みましょう
4.45
試験で使われる問題用紙はかなり大きめ。同じ大きさで過去問を用意して本番感覚を養いましょう。印刷するのはパパとママの役目。A3ノビまで対応、全色顔料インクで滲まない。最大給紙枚数は550枚。
解答
- 解答を開く
-
1辺が1cmの立方体をすきまなく積み重ねて，右の図のような立体をつくりました。次の問いに答えなさい。
（1） 立方体の数は何個以上何個以下といえますか。
（2） 立方体の数がもっとも多い個数となるとき，この立体の表面積を求めなさい。（1）
【一番少なる場合】
AとBの片方が4個、もう一方が1個、
CとDの片方が3個、もう一方が1個、
E、F、Gのどれか1つが2個、残りは1個という積み方になればよい。よって、13個。
【一番多くなる場合】
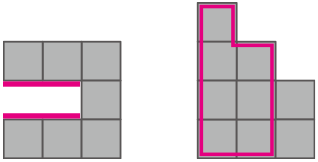
上から見た平面図に積み重ねる立方体の数を書くと分かり易い。20個。（答え） 13個以上20以下
（2）
前後左右上下から見える部分の表面積は、7×2＋9×2＋10×2＝52cm2
内側に隠れている部分の表面積は、4×2＋3×2＝14cm2
合わせて、52＋14＝66cm2
（答え） 66cm2
【一番少なる場合】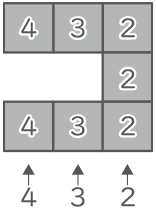
【一番多くなる場合】
ではまた～
