問題
図1の一辺の長さが6cmの立方体の中に,一辺の長さが2cmの立方体を積み上げて立体㋐を作りました。立体㋐を図1の真上から見たときに,それぞれの場所に積まれた立方体の個数を表1に表します。例えば,図2の立体のときは表2となります。このとき,次の各問いに答えなさい。
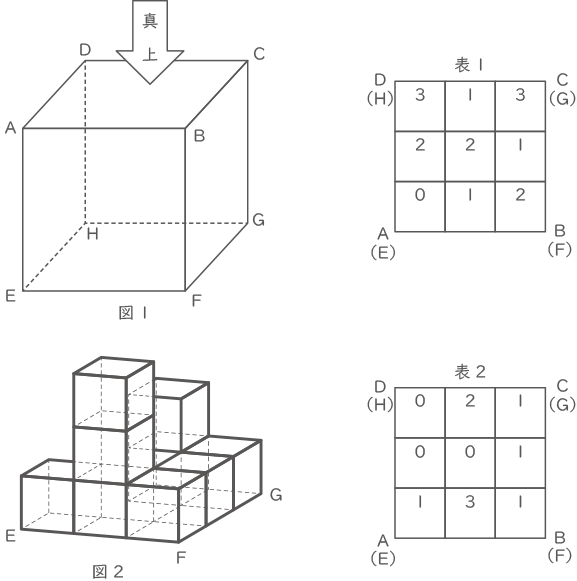
(1) 立体㋐の表面積を求めなさい。
(2) 立体㋐を3点B,C,Eを通る平面で切断したとき,大きい方の立体の体積を求めなさい。
(3) (2)で体積を求めた立体をさらに,3点B,F,Hを通る平面で切断したとき,大きい方の立体の体積を求めなさい。ただし,(三角すいや四角すいの体積)=(底面の面積)×(高さ)÷3です。
これまでほとんどの通信教育で実現できなかった難関国私立中学合格。Z会なら、可能です。【公立中高一貫校を受検予定 】の方は試しに資料請求してみましょう。HPにも「小学生コース専科 公立中高一貫校受検対策講座のご案内」が詳しく記載されています。
解答
- 解答を開く
-
図1の一辺の長さが6cmの立方体の中に,一辺の長さが2cmの立方体を積み上げて立体㋐を作りました。立体㋐を図1の真上から見たときに,それぞれの場所に積まれた立方体の個数を表1に表します。例えば,図2の立体のときは表2となります。このとき,次の各問いに答えなさい。

(1) 立体㋐の表面積を求めなさい。
(2) 立体㋐を3点B,C,Eを通る平面で切断したとき,大きい方の立体の体積を求めなさい。
(3) (2)で体積を求めた立体をさらに,3点B,F,Hを通る平面で切断したとき,大きい方の立体の体積を求めなさい。ただし,(三角すいや四角すいの体積)=(底面の面積)×(高さ)÷3です。(1)
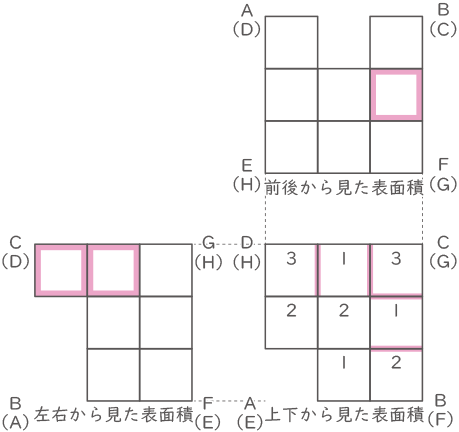
前後から見た表面積2×2×8=32
左右から見た表面積2×2×7=28
上下から見た表面積2×2×8=32
見えるところの表面積合計は(32+28+32)×2=184cm2
見えない表面積は赤線の部分で2×2×6=24cm2
合わせて184+24=208cm2
(答え) 208cm2
(2)
Gを含む側の体積を求める。
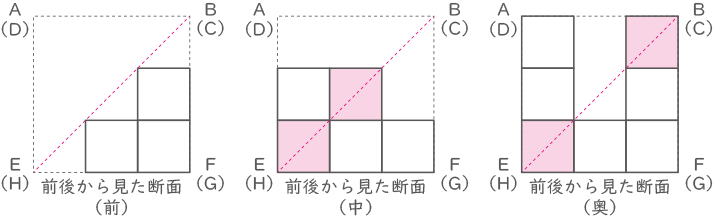
前後から見た断面(前) 2×2×2×3=24
前後から見た断面(中) (2×2×2×2)+(2×2×$ \displaystyle \frac{1}{2} $×2×2)=24
前後から見た断面(奥) (2×2×2×3)+(2×2×$ \displaystyle \frac{1}{2} $×2×2)=32
合わせて24+24+32=80cm3
(答え) 80cm3
(3)
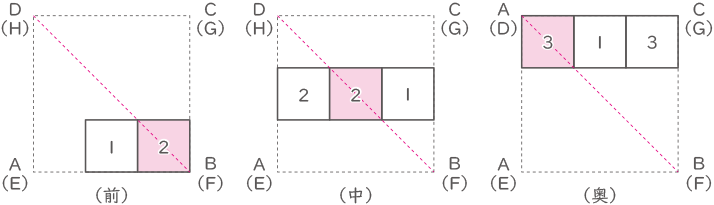
問(2)の3図を上から見る。
数字はそれぞれの場所に積まれた立方体の個数。
Gを含む側の体積を調べる。
(前)2×2×$ \displaystyle \frac{1}{2} $×4=8
(中)(2×2×2)+(2×2×$ \displaystyle \frac{1}{2} $×2)+(2×2×2×$ \displaystyle \frac{1}{3} $)=14$ \displaystyle \frac{2}{3} $
(奥)(2×2×2×3)+(2×2×$ \displaystyle \frac{1}{2} $×2)+(2×2×2×$ \displaystyle \frac{1}{3} $)=30$ \displaystyle \frac{2}{3} $
合わせて8+14$ \displaystyle \frac{2}{3} $+30$ \displaystyle \frac{2}{3} $=53$ \displaystyle \frac{1}{3} $cm3・・・Gを含む側の体積の方が大きい(答え) 53$ \displaystyle \frac{1}{3} $cm3