問題
下の図は1辺の長さが6cmの立方体で,DJ=3cm,BI=2cmです。
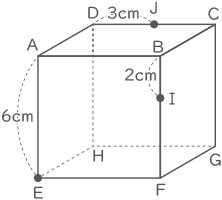
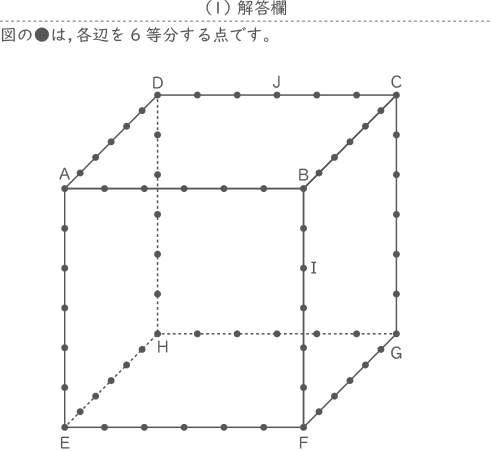
(1) 点E,J,Iを通る平面でこの立方体を切断するとき,切断面の線を解答用紙の立方体に書き込みなさい。ただし,裏側の線も書くこと。
(2) 点E,J,Iを通る平面でこの立方体を切断するとき,点Gを含む立体の体積を求めなさい。
(3) (2)の点Gを含む立体をさらに点D,B,Fを通る平面で切断したとき,点Gを含む立体の体積を求めなさい。
Amazonブランドのタブレット[Fire HD 10 Plus タブレット10.1インチ]フルHDディスプレイ(1920×1200)だから広くて見やすく家勉の必需品。
解答
- 解答を開く
-
下の図は1辺の長さが6cmの立方体で,DJ=3cm,BI=2cmです。

(1) 点E,J,Iを通る平面でこの立方体を切断するとき,切断面の線を解答用紙の立方体に書き込みなさい。ただし,裏側の線も書くこと。
(2) 点E,J,Iを通る平面でこの立方体を切断するとき,点Gを含む立体の体積を求めなさい。
(3) (2)の点Gを含む立体をさらに点D,B,Fを通る平面で切断したとき,点Gを含む立体の体積を求めなさい。
 (1)
(1)
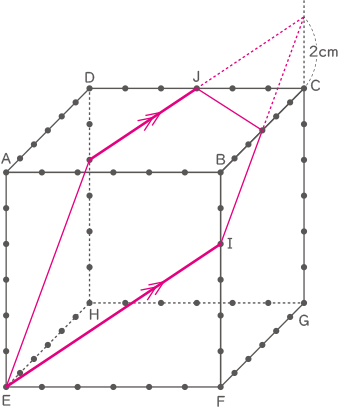
断面内にE,I,Jがあるので、EIに平行でJを通る線をつくり、さらに延長する。(答え) 図の赤い実線が切断面の線
 (2)
(2)
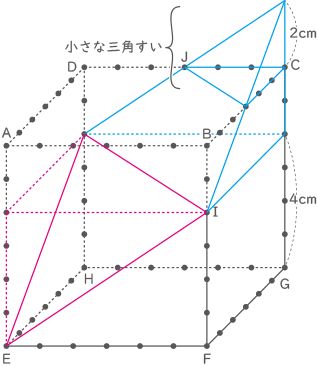
赤い三角すいと青い三角すいは体積が同じ。
よって、高さ4cmの四角柱の体積から小さな三角すいの体積を引く。
6×6×4-3×3×$ \displaystyle \frac{1}{2} $×2×$ \displaystyle \frac{1}{3} $=141cm3(答え) 141cm3
 (3)
(3)
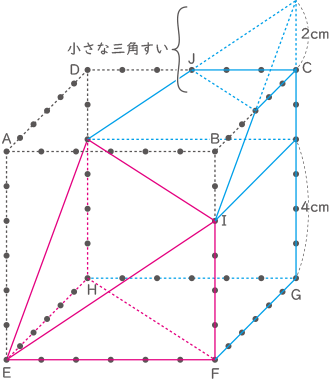
青い図形の下部(三角柱)と上部(三角すい台)に分けて体積を求める。
下部の体積
6×6×$ \displaystyle \frac{1}{2} $×4=72cm3
上部の体積
小さな三角すいの体積3×3×$ \displaystyle \frac{1}{2} $×2×$ \displaystyle \frac{1}{3} $=3cm3
3×(2×2×2-1)=21cm3
(相似な立体の体積比1:8を利用)合わせて72+21=93cm3
(答え) 93cm3


 (1)
(1) (2)
(2) (3)
(3)








