問題
次の各問いに答えなさい。必要であれば、円周率を3.14として計算しなさい。
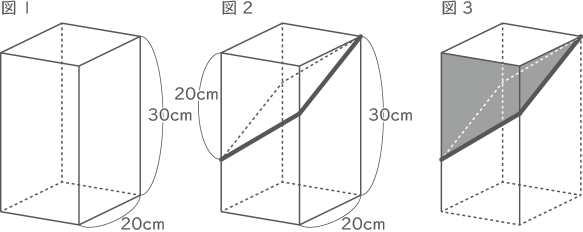
(1) 図1のような底面が1辺20cmの正方形で、高さが30cmの直方体がありました。この直方体の側面のみをペンキで塗りました。次に図2のように切り口が平面になるような太線で直方体を切ったとき、小さい方の立体のペンキで塗られた部分の面積を求めなさい。
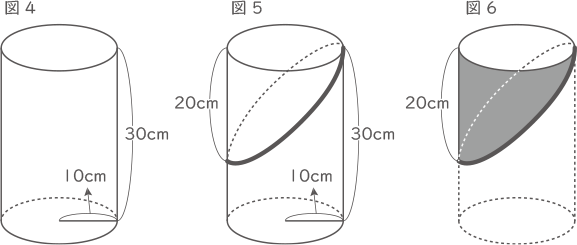
(2) 図4のような底面の半径が10cm、高さが30cmの円柱がありました。この円柱の側面のみをペンキで塗り、図5のように切り口が平面になるような太線で円柱を切ったとき、小さい方の立体のペンキで塗られた部分の面積を求めなさい。
灘をはじめ、名だたる難関中学に毎年多数の合格者を出す「浜学園」。講師の質や、教材のよさは折り紙付き。引きつりそうな料金設定ですが、中学受験をすると決めたら偏差値を買うんだ!ぐらいの前向きな気持ちで行きましょう。気になる方は資料請求してお子さんに合いそうか是非確認してみましょう。もちろん、体験入塾も無料で用意されています。
解答
- 解答を開く
-
次の各問いに答えなさい。必要であれば、円周率を3.14として計算しなさい。
(1) 図1のような底面が1辺20cmの正方形で、高さが30cmの直方体がありました。この直方体の側面のみをペンキで塗りました。次に図2のように切り口が平面になるような太線で直方体を切ったとき、小さい方の立体のペンキで塗られた部分の面積を求めなさい。

(2) 図4のような底面の半径が10cm、高さが30cmの円柱がありました。この円柱の側面のみをペンキで塗り、図5のように切り口が平面になるような太線で円柱を切ったとき、小さい方の立体のペンキで塗られた部分の面積を求めなさい。

(1)
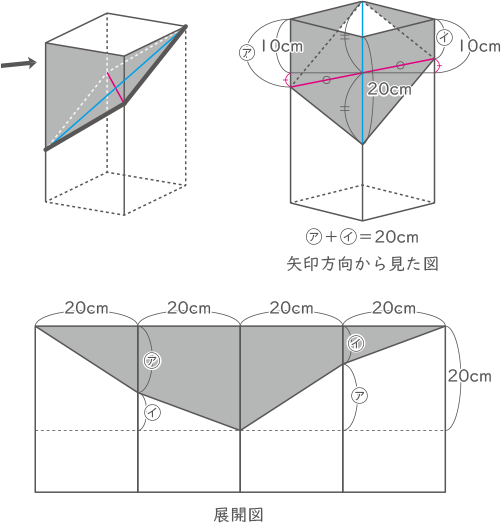
下の解説図の通りとなるので、
40×20=800cm2
(答え) 800cm2
(2)
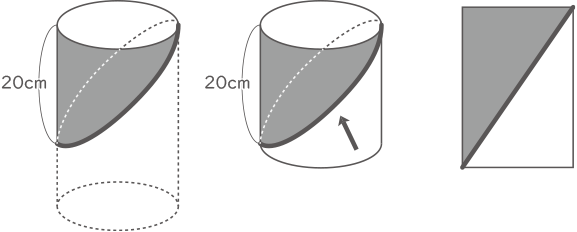
下の解説図の通り、高さを20cmとして見ると分かり易い。
円柱を2等分したことになり、求める面積は側面積の半分となる。
10×2×3.14×20÷2=628cm2
(答え) 628cm2