問題
次の問いに答えなさい。
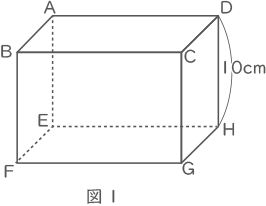 (1) 図1のような、高さが10cmの直方体ABCD-EFGHがあります。
(1) 図1のような、高さが10cmの直方体ABCD-EFGHがあります。
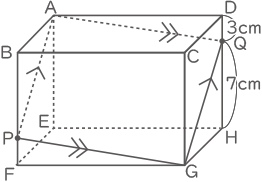
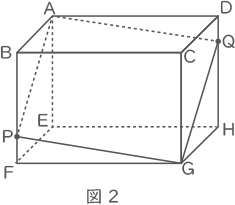 この直方体を、図2のように、頂点Aと頂点Gの両方を通る平面で切断したところ、平面が辺BF上の点Pと、辺DH上の点Qで交わり、QH=7cmでした。
この直方体を、図2のように、頂点Aと頂点Gの両方を通る平面で切断したところ、平面が辺BF上の点Pと、辺DH上の点Qで交わり、QH=7cmでした。
PFの長さは何cmですか。
(2) 図3のような、高さが10cmの四角柱ABCD-EFGHがあります。四角形ABCDは、縦4cm,横15cmの長方形から図4のように2つの直角三角形を切り取った台形です。
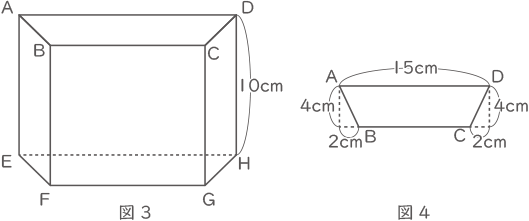
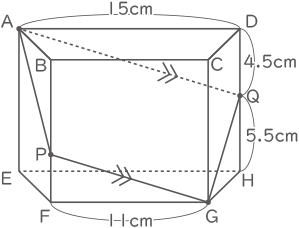
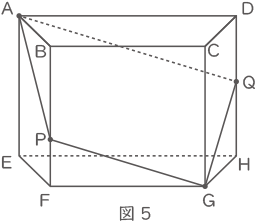 この四角柱を、図5のように、頂点Aと頂点Gの両方を通る平面で切断したところ、平面が辺BF上の点Pと、辺DH上の点Qで交わり、QH=5.5 cmでした。
この四角柱を、図5のように、頂点Aと頂点Gの両方を通る平面で切断したところ、平面が辺BF上の点Pと、辺DH上の点Qで交わり、QH=5.5 cmでした。
① PGの長さはAQの長さの何倍ですか。
② PFの長さは何cmですか。
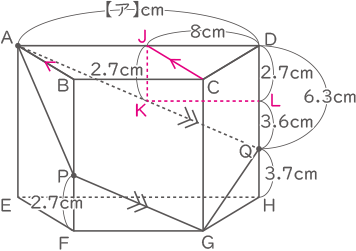
(3) 図6のような、高さが10cmの四角柱ABCD-EFGHがあります。四角形ABCDは、縦4cm,横【ア】cmの長方形から図7のように2つの直角三角形を切り取った台形です。
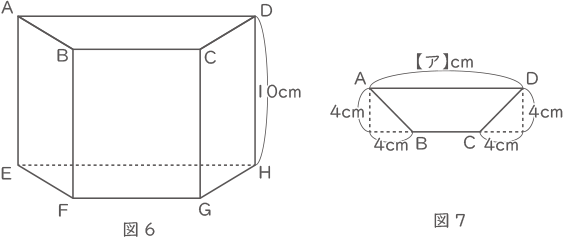
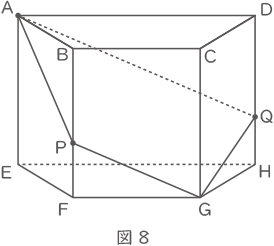 この四角柱を、図8のように、頂点Aと頂点Gの両方を通る平面で切断したところ、平面が辺BF上の点Pと、辺DH上の点Qで交わり、PF=2.7cm,QH=3.7cmでした。
この四角柱を、図8のように、頂点Aと頂点Gの両方を通る平面で切断したところ、平面が辺BF上の点Pと、辺DH上の点Qで交わり、PF=2.7cm,QH=3.7cmでした。
【ア】にあてはまる数を求めなさい。途中(とちゅう)の式や考え方なども書きなさい。
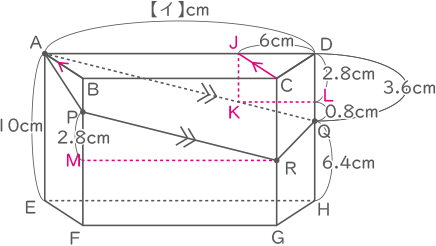
(4) 図9のような、高さが10cmの四角柱ABCD-EFGHがあります。四角形ABCDは、縦4cm, 横【イ】cmの長方形から図10のように2つの直角三角形を切り取った台形です。
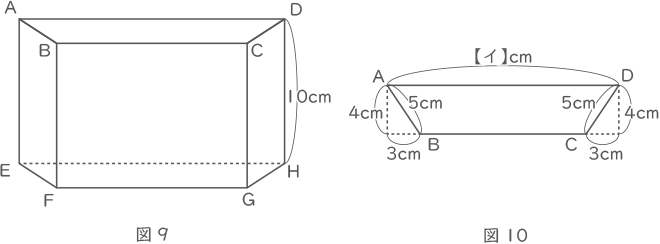
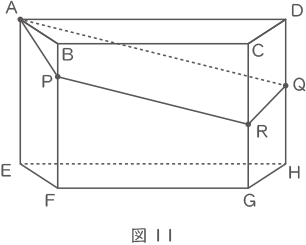 この四角柱を、図11のように、頂点Aを通る平面で切断したところ、平面が辺BF,CG,DHとそれぞれP,R,Qで交わり、QH=6.4cmで、台形AEFPと台形RGHQの面積の差が16cm2でした。
この四角柱を、図11のように、頂点Aを通る平面で切断したところ、平面が辺BF,CG,DHとそれぞれP,R,Qで交わり、QH=6.4cmで、台形AEFPと台形RGHQの面積の差が16cm2でした。
① PFの長さとRGの長さの差は何cmですか。
② 【イ】にあてはまる数を求めなさい。
試験で使われる問題用紙はかなり大きめ。同じ大きさで過去問を用意して本番感覚を養いましょう。印刷するのはパパとママの役目。A3ノビまで対応、全色顔料インクで滲まない。最大給紙枚数は550枚。
解答
- 解答を開く
-
次の問いに答えなさい。
 (1) 図1のような、高さが10cmの直方体ABCD-EFGHがあります。
(1) 図1のような、高さが10cmの直方体ABCD-EFGHがあります。 この直方体を、図2のように、頂点Aと頂点Gの両方を通る平面で切断したところ、平面が辺BF上の点Pと、辺DH上の点Qで交わり、QH=7cmでした。
この直方体を、図2のように、頂点Aと頂点Gの両方を通る平面で切断したところ、平面が辺BF上の点Pと、辺DH上の点Qで交わり、QH=7cmでした。
PFの長さは何cmですか。(2) 図3のような、高さが10cmの四角柱ABCD-EFGHがあります。四角形ABCDは、縦4cm,横15cmの長方形から図4のように2つの直角三角形を切り取った台形です。

 この四角柱を、図5のように、頂点Aと頂点Gの両方を通る平面で切断したところ、平面が辺BF上の点Pと、辺DH上の点Qで交わり、QH=5.5 cmでした。
この四角柱を、図5のように、頂点Aと頂点Gの両方を通る平面で切断したところ、平面が辺BF上の点Pと、辺DH上の点Qで交わり、QH=5.5 cmでした。
① PGの長さはAQの長さの何倍ですか。
② PFの長さは何cmですか。(3) 図6のような、高さが10cmの四角柱ABCD-EFGHがあります。四角形ABCDは、縦4cm,横【ア】cmの長方形から図7のように2つの直角三角形を切り取った台形です。

 この四角柱を、図8のように、頂点Aと頂点Gの両方を通る平面で切断したところ、平面が辺BF上の点Pと、辺DH上の点Qで交わり、PF=2.7cm,QH=3.7cmでした。
この四角柱を、図8のように、頂点Aと頂点Gの両方を通る平面で切断したところ、平面が辺BF上の点Pと、辺DH上の点Qで交わり、PF=2.7cm,QH=3.7cmでした。
【ア】にあてはまる数を求めなさい。途中(とちゅう)の式や考え方なども書きなさい。(4) 図9のような、高さが10cmの四角柱ABCD-EFGHがあります。四角形ABCDは、縦4cm, 横【イ】cmの長方形から図10のように2つの直角三角形を切り取った台形です。

 この四角柱を、図11のように、頂点Aを通る平面で切断したところ、平面が辺BF,CG,DHとそれぞれP,R,Qで交わり、QH=6.4cmで、台形AEFPと台形RGHQの面積の差が16cm2でした。
この四角柱を、図11のように、頂点Aを通る平面で切断したところ、平面が辺BF,CG,DHとそれぞれP,R,Qで交わり、QH=6.4cmで、台形AEFPと台形RGHQの面積の差が16cm2でした。
① PFの長さとRGの長さの差は何cmですか。
② 【イ】にあてはまる数を求めなさい。 (1)
(1)
三角形ADQと三角形GFPは3つの角が同じで、AD=GFなので合同。よって、RF=QD=3cm。(答え) 3cm
 (2)―①
(2)―①
三角形ADQと三角形GFPは3つの角が同じことより相似。
AD:GF=15:11=AQ:PG
AQ×11=PG×15
PG=$ \displaystyle \frac{11}{15} $×AQ(答え) $ \displaystyle \frac{11}{15} $倍
(2)―②
QD=4.5cmなので①と同様に比から長さを求める。
PF=$ \displaystyle \frac{11}{15} $×QD=$ \displaystyle \frac{11}{15} $×4.5=3.3cm(答え) 3.3cm
(3)
Cを通り、ABに平行な直線がADと交わる点をJとする。
次に、Jから垂直に下した直線がAQと交わる点をKとする。
さらに、Kを通り、ADと平行な直線がDHと交わる点をLとする。
三角形AJKと三角形GFPは合同なのでKJ=PF=2.7cm
三角形ADQと三角形KLQは相似なので、3.6cm:6.3cm=KL(8cm):AD
よって、ADは14cm。
(答え) 14
(4)―①
台形AEFPの面積=(10+PF)×5÷2=25+PF×2.5
台形RGHQの面積=(6.4+RG)×5÷2=16+RG×2.5
面積差16cm2より、
9+PF×2.5-RG×2.5=16
PF-RG=2.8cm・・・PFの長さとRGの長さの差(答え) 2.8cm
(4)―②
(3)と同様の手順で、各点J,K,Lを作る。
さらに、Rを通り、ADに平行な直線がBFと交わる点をMとする。
三角形AJKと三角形RMPは合同なのでMP=JK=DL=2.8cm、LQ=0.8cmとなる。
三角形ADQと三角形KLQは相似なので、0.8cm:6cm=3.6cm:【イ】
【イ】の長さは27cm。
(答え) 27


 (1)
(1) (2)―①
(2)―①