立体の切断-2-1（駒場東邦中学2014/2度切断した立方体の展開図）

問題

 問題（駒場東邦中学2014/2度切断した立方体の展開図）

 

図のような一辺の長さが2cmの立方体をいくつかの平面で切って作られる立体について考えます。

この立方体を3点A，C，Fを通る平面と3点A，C，Hを通る平面で切って，面EFGHを含む方を1つめの立体とします。

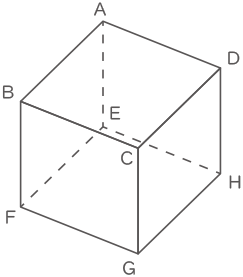
2つめの立体は，この立方体を3点A，C，Fを通る平面，3点A，C，Hを通る平面，3点B，D，Eを通る平面と3点B，D，Gを通る平面で切って，面EFGHを含む方の立体とします。

（1） 1つめの立体の体積を求めなさい。ただし，角すいの体積は（底面積） x（高さ）÷3で求めることができます。

（2） 2つめの立体の面はどのような図形がいくつあるか答えなさい。
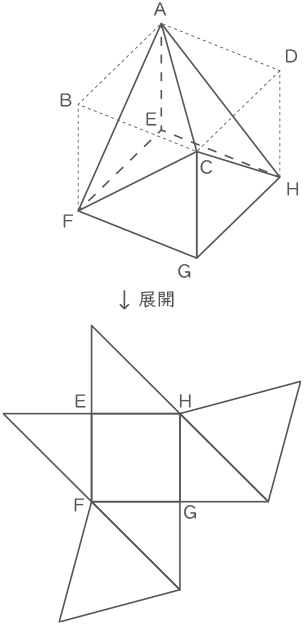
例えば1つめの立体は展開図が右図のようになるので，
【正方形　1つ，正三角形　2つ，直角二等辺三角形　4つ】
となります。答えはこのような形で書きなさい。

（3） 1つめの立体の表面積から2つめの立体の表面積を引いた値を求めなさい。

解答

 解答を開く

 

図のような一辺の長さが2cmの立方体をいくつかの平面で切って作られる立体について考えます。

この立方体を3点A，C，Fを通る平面と3点A，C，Hを通る平面で切って，面EFGHを含む方を1つめの立体とします。

2つめの立体は，この立方体を3点A，C，Fを通る平面，3点A，C，Hを通る平面，3点B，D，Eを通る平面と3点B，D，Gを通る平面で切って，面EFGHを含む方の立体とします。

（1） 1つめの立体の体積を求めなさい。ただし，角すいの体積は（底面積） x（高さ）÷3で求めることができます。

（2） 2つめの立体の面はどのような図形がいくつあるか答えなさい。
例えば1つめの立体は展開図が右図のようになるので，
【正方形　1つ，正三角形　2つ，直角二等辺三角形　4つ】
となります。答えはこのような形で書きなさい。

（3） 1つめの立体の表面積から2つめの立体の表面積を引いた値を求めなさい。

 

---

 

（1）

2×2×2－2×2×$ \displaystyle \frac{1}{2} $×2×$ \displaystyle \frac{1}{3} $×2＝$ \displaystyle \frac{16}{3} $=5$ \displaystyle \frac{1}{3} $

 

（答え）　5$ \displaystyle \frac{1}{3} $cm³

 

＜補助線を引き、考え易くしてみる＞

（2）

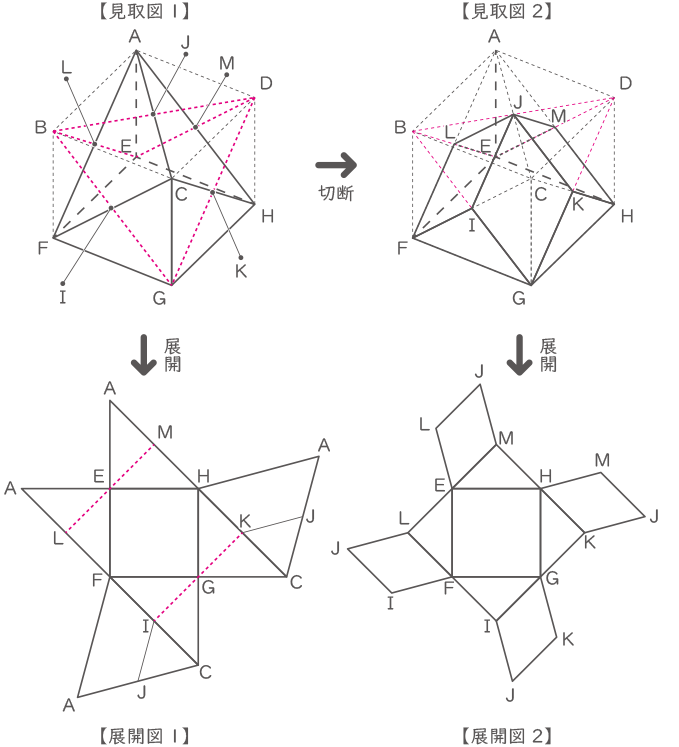
【見取図1】より、三角形BDGは正三角形で、その各辺の真ん中の3点を結んだ三角形IJKも正三角形。よって、【見取図2】より、面IJKGは正三角形IJKと正三角形IGKでできたひし形。
【見取図2】を展開した【展開図2】より、「正方形　1つ、直角二等辺三角形　4つ、ひし形　4つ」となる。

（答え）　正方形　1つ、直角二等辺三角形　4つ、ひし形　4つ

 

（3）

【展開図1】の正三角形ACFは、【展開図2】のひし形IJKGの倍の面積なので、【展開図1】の面積と【展開図2】の面積の差は、【展開図1】の三角形CIGの面積の4つ分となる。
（2×2÷4）×4＝4cm²

 

（答え）　4cm²