問題
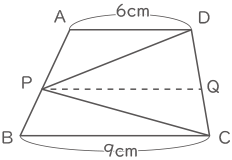
左図の台形 ABCD は，ADとBC が平行で，AD=6cm，BC=9cmです。辺 AB上に点 Pをとると，三角形PCDと台形ABCDの面積比が5：9でした。
このとき、次の問いに答えなさい。
（1） 点 P をとおり，ADに平行な直線と辺CDとの交点をQとするとき，PQの長さを求めなさい。
（2） AP：PBを最もかんたんな整数の比で表しなさい。
教室には遠くて通えない、通塾負担を減らしたい。もしくは他の習い事が忙しくて、通塾の時間が取れない・・・ そんなご家庭に最適！ 4大塾に通いながら弱点補強を家庭教師に任せているご家庭も多々、塾のクラスを上げるためにピンポイントでうまく利用しましょう。なにはともあれ資料請求してお子さんに合うか見てみましょう。
解答
- 解答を開く
-
左図の台形 ABCD は，ADとBC が平行で，AD=6cm，BC=9cmです。辺 AB上に点 Pをとると，三角形PCDと台形ABCDの面積比が5：9でした。
このとき、次の問いに答えなさい。（1） 点 P をとおり，ADに平行な直線と辺CDとの交点をQとするとき，PQの長さを求めなさい。
（2） AP：PBを最もかんたんな整数の比で表しなさい。
（1）
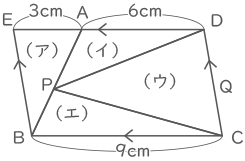
図の様に、辺ADの延長線上で平行四辺形をつくれるところに点Eをおき、4つの三角形の面積を（ア）、（イ）、（ウ）、（エ）として面積比を考える。（ア）：（イ）＋（ウ）＋（エ）＝1：5
（イ）＋（エ）：（ウ）＝4：5
数字をそろえると、（・・・連比を使って）
（ア）：（イ）＋（ウ）＋（エ）＝9：45
（イ）＋（エ）：（ウ）＝20：25
平行四辺形の面積が54（＝9＋45）、点Pが辺BE上にある場合には（ウ）の面積が27（＝54÷2）になるが、実際には25なので、
PQの長さ＝9×$ \displaystyle \frac{25}{27} $＝8$ \displaystyle \frac{1}{3} $cm（答え） 8$ \displaystyle \frac{1}{3} $cm
（2）
辺BAと辺CDを延長してできる交点を点Fとする。CF：DF＝9：6より、その他の長さの比も図の様にわかるので、AP：PB＝2$ \displaystyle \frac{1}{3} $：$ \displaystyle \frac{2}{3} $＝7：2（答え） 7：2
図の様に、辺ADの延長線上で平行四辺形をつくれるところに点Eをおき、4つの三角形の面積を（ア）、（イ）、（ウ）、（エ）として面積比を考える。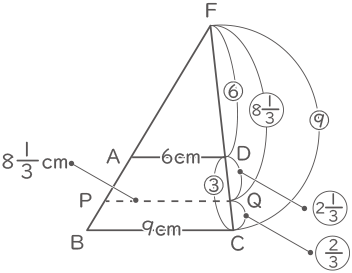
辺BAと辺CDを延長してできる交点を点Fとする。CF：DF＝9：6より、その他の長さの比も図の様にわかるので、AP：PB＝2$ \displaystyle \frac{1}{3} $：$ \displaystyle \frac{2}{3} $＝7：2
