問題
S君は球場に野球観戦に行きました。球場には一定の割合で観客が集まってきます。午後5時45分に開場したときには,何人かの列ができていました。
人場ゲートを5か所にすると48分で列はなくなり,入場ゲートを8か所にすると24分で列はなくなります。
(1) 開場後,午後6 時までに列をなくすには,少なくとも□か所の入場ゲートが必要です。
(2) 開場後,はじめは入場ゲートを5か所にしていましたが,途中で8か所にしたところ,開場から33分後に列はなくなりました。入場ゲートを8か所にしたのは開場から□分後です。
試験で使われる問題用紙はかなり大きめ。同じ大きさで過去問を用意して本番感覚を養いましょう。印刷するのはパパとママの役目。A3ノビまで対応、全色顔料インクで滲まない。最大給紙枚数は550枚。
解答
- 解答を開く
-
S君は球場に野球観戦に行きました。球場には一定の割合で観客が集まってきます。午後5時45分に開場したときには,何人かの列ができていました。
人場ゲートを5か所にすると48分で列はなくなり,入場ゲートを8か所にすると24分で列はなくなります。(1) 開場後,午後6 時までに列をなくすには,少なくとも□か所の入場ゲートが必要です。
(2) 開場後,はじめは入場ゲートを5か所にしていましたが,途中で8か所にしたところ,開場から33分後に列はなくなりました。入場ゲートを8か所にしたのは開場から□分後です。
(1)
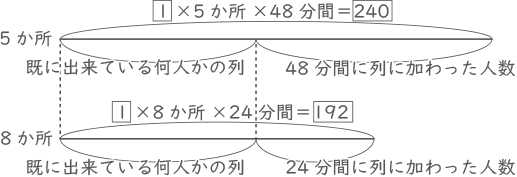
ニュートン算の処理手順を知っている事。また数字を変えた時にも対応できるかも問われる。入場ゲート1か所で1分間に処理できる人数を$ \fbox{1} $とする。

48-24=24分間で$ \fbox{240} $-$ \fbox{192} $=$ \fbox{48} $の人数が新たに列に加わるので、1分間当たり$ \fbox{2} $の人数が列に加わる。
既に出来ている何人かの列=$ \fbox{240} $-$ \fbox{2} $×48=$ \fbox{144} $15分後の午後6時丁度に列が無くなる入場ゲート数を△として線分図をつくる。

$ \fbox{144} $+$ \fbox{2} $×15=$ \fbox{15} $×△
△=$ \fbox{\( \displaystyle \frac{174}{15} \)} $=11.6
11か所では午後6時までに列は無くならず、12か所であれば午後6時前に列が無くなる。(答え) 12
(2)
つるかめ算的に数字を少しずつ変えてゆくのは面倒なので数直線で考える。入場ゲートを8か所にしている時間を〇分、5か所にしている時間を(33-〇)分として線分図をつくる。

$ \fbox{144} $+$ \fbox{2} $×33=$ \fbox{1} $×5×(33-〇)+$ \fbox{1} $×8×〇
$ \fbox{210} $=$ \fbox{165} $-$ \fbox{5} $×〇+$ \fbox{8} $×〇
$ \fbox{45} $=$ \fbox{3} $×〇
〇=15
よって、入場ゲートを8か所にしている時間は15分間で、入場ゲートを5か所にしている時間は18分間、つまり18分後。(答え) 18