問題
ある日,大雨が降り続いたためにダムの貯水率が90%になってしまいました。
雨が降り続いている中,ダムの貯水率を60%にするために放水を始めました。
2つの門を使って放水すると15時間で貯水率が60%になり,3つの門を使って放水すると5時間で貯水率が60%になります。放水性能が半分である予備の門も合わせた4つの門を使って放水するとき,貯水率が90%の状態から放水すると貯水率が60%になるまでに何時間何分かかりますか。
教室には遠くて通えない、通塾負担を減らしたい。もしくは他の習い事が忙しくて、通塾の時間が取れない・・・ そんなご家庭に最適! 4大塾に通いながら弱点補強を家庭教師に任せているご家庭も多々、塾のクラスを上げるためにピンポイントでうまく利用しましょう。なにはともあれ資料請求してお子さんに合うか見てみましょう。
解答
- 解答を開く
-
ある日,大雨が降り続いたためにダムの貯水率が90%になってしまいました。
雨が降り続いている中,ダムの貯水率を60%にするために放水を始めました。
2つの門を使って放水すると15時間で貯水率が60%になり,3つの門を使って放水すると5時間で貯水率が60%になります。放水性能が半分である予備の門も合わせた4つの門を使って放水するとき,貯水率が90%の状態から放水すると貯水率が60%になるまでに何時間何分かかりますか。1つの門の1時間あたりの排水量を$ \fbox{2} $とする。
予備の門の1時間あたりの排水量を$ \fbox{1} $とする。
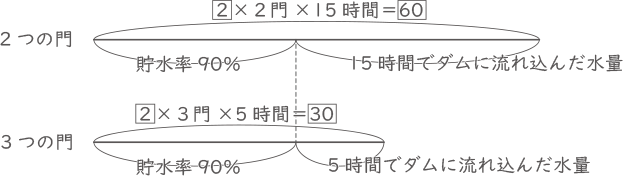
線分図より、
貯水率90%+15時間でダムに流れ込んだ水量=$ \fbox{60} $
貯水率90%+5時間でダムに流れ込んだ水量=$ \fbox{30} $
2式の差より、10時間でダムに流れ込んだ水量は$ \fbox{30} $とわかるので、5時間でダムに流れ込んだ水量は$ \fbox{15} $、貯水率90%は$ \fbox{15} $とわかる。放水性能が半分である予備の門も合わせた4つの門を使って放水すると、その量は$ \fbox{2} $×3+$ \fbox{1} $=$ \fbox{7} $ 。
1時間あたりにダムに流れ込む水量は$ \fbox{3} $ 。
これを線分図にすると、
$ \fbox{15} $+$ \fbox{3} $×〇=$ \fbox{7} $×〇
$ \fbox{15} $=$ \fbox{4} $×〇
〇=$ \displaystyle \frac{15}{4} $=3$ \displaystyle \frac{3}{4} $=3$ \displaystyle \frac{45}{60} $よって、3時間45分。
(答え) 3時間45分