問題
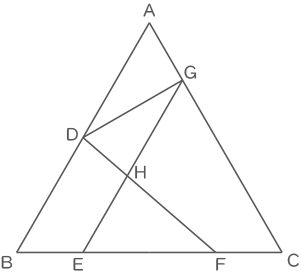 右の図の三角形ABCは正三角形で,AD:DB=1:1,BE:EF:FC=1:2:1,CG:GA=3:1です。次の問いに答えなさい。
右の図の三角形ABCは正三角形で,AD:DB=1:1,BE:EF:FC=1:2:1,CG:GA=3:1です。次の問いに答えなさい。
(1) DH:HFを最も簡単な整数の比で答えなさい。
(2) 三角形EFHと三角形ABCの面積の比を最も簡単な整数の比で答えなさい。
(3) 三角形DHGと三角形ABCの面積の比を最も簡単な整数の比で答えなさい。
(4) EH:HGを最も簡単な整数の比で答えなさい。
試験で使われる問題用紙はかなり大きめ。同じ大きさで過去問を用意して本番感覚を養いましょう。印刷するのはパパとママの役目。A3ノビまで対応、全色顔料インクで滲まない。最大給紙枚数は550枚。
解答
- 解答を開く
-
 右の図の三角形ABCは正三角形で,AD:DB=1:1,BE:EF:FC=1:2:1,CG:GA=3:1です。次の問いに答えなさい。
右の図の三角形ABCは正三角形で,AD:DB=1:1,BE:EF:FC=1:2:1,CG:GA=3:1です。次の問いに答えなさい。(1) DH:HFを最も簡単な整数の比で答えなさい。
(2) 三角形EFHと三角形ABCの面積の比を最も簡単な整数の比で答えなさい。
(3) 三角形DHGと三角形ABCの面積の比を最も簡単な整数の比で答えなさい。
(4) EH:HGを最も簡単な整数の比で答えなさい。 (1)
(1)
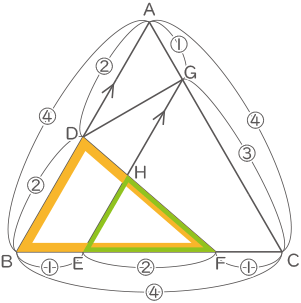
AG:GC=BE:EC=①:③よりBAとEGは平行なので△FBDと△FEHは相似。
BE:EF=①:②なのでDH:HF=1:2(答え) 1:2
 (2)
(2)
(辺の比から面積比を求める)
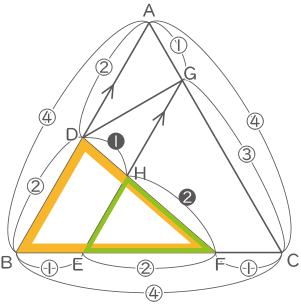
△ABCの面積×$ \displaystyle \frac{②}{④} $×$ \displaystyle \frac{③}{④} $=△DBFの面積
△ABCの面積×$ \displaystyle \frac{3}{8} $=△DBFの面積
△DBFの面積×$ \displaystyle \frac{②}{③} $×$ \displaystyle \frac{❷}{❸} $=△EFHの面積
△DBFの面積×$ \displaystyle \frac{4}{9} $=△EFHの面積
このことより、
△ABCの面積×$ \displaystyle \frac{1}{6} $=△EFHの面積
三角形EFHと三角形ABCの面積の比=1:6(答え) 1:6
 (3)
(3)
(辺の比から面積比を求める)
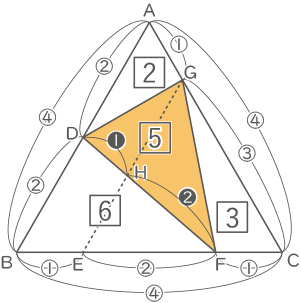
△ABCの面積=④×④=$ \fbox{16} $
△ADGの面積=①×②=$ \fbox{2} $
△DBFの面積=②×③=$ \fbox{6} $
△GFCの面積=①×③=$ \fbox{3} $
△GDFの面積=$ \fbox{16} $-$ \fbox{2} $-$ \fbox{6} $-$ \fbox{3} $=$ \fbox{5} $△DHGの面積=△GDFの面積×$ \displaystyle \frac{❶}{❸} $=$ \fbox{5} $×$ \displaystyle \frac{1}{3} $=$ \fbox{\( \displaystyle \frac{5}{3} \)} $
△DHGの面積:△ABCの面積=$ \fbox{\( \displaystyle \frac{5}{3} \)} $:$ \fbox{16} $=5:48(答え) 5:48
 (4)
(4)
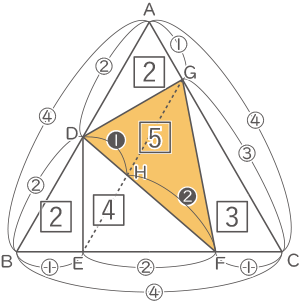
△DBEの面積=②×①=$ \fbox{2} $
△DEFの面積=$ \fbox{6} $-$ \fbox{2} $=$ \fbox{4} $
△DEFと△GDFの底辺をDFとすると、面積比が4:5なので高さの比EH:HGも$ \fbox{4} $:$ \fbox{5} $(答え) 4:5


 (1)
(1) (2)
(2) (3)
(3) (4)
(4)








