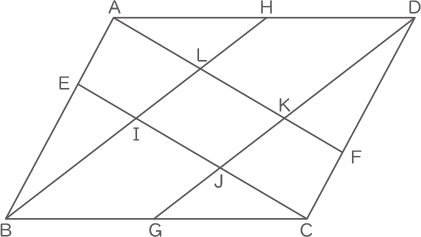
面積比-2-4（海城中学2022/三角形の相似から比を出して面積を求めよう）

1 問題
2 解答

問題

問題（海城中学2022/三角形の相似から比を出して面積を求めよう）

下の図のように，平行四辺形 ABCDの辺ABを1：2に分ける点をE，辺 CDを1：2に分ける点を Fとし，辺BCと辺 DAの真ん中の点をそれぞれG，Hとします。
また，BHとCEが交わる点をI，CEとDGが交わる点をJ，DGとAFが交わる点をK，AFとBHが交わる点をLとします。次の問いに答えなさい。

（1） BI：IL：LHを最も簡単な整数の比で答えなさい。
（2）平行四辺形ABCDと四角形IJKLの面積の比を最も簡単な整数の比で答えなさい。
（3）平行四辺形ABCDと四角形AEILの面積の比を最も簡単な整数の比で答えなさい。

教室には遠くて通えない、通塾負担を減らしたい。もしくは他の習い事が忙しくて、通塾の時間が取れない・・・そんなご家庭に最適！　4大塾に通いながら弱点補強を家庭教師に任せているご家庭も多々、塾のクラスを上げるためにピンポイントでうまく利用しましょう。なにはともあれ資料請求してお子さんに合うか見てみましょう。

解答

解答を開く

（1）
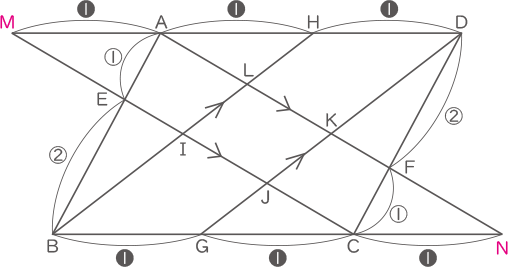
線を延長し、交点をM，Nとする。

線を延長し、交点をM，Nとする。
三角形MEAと三角形AFDが相似なことより、MAの比は❶となり、同様にNCも❶となる。
三角形IHMと三角形IBCは合同なのでIB＝IHで、IB：IH＝2：2となる。・・・㋐
三角形LHAと三角形LBNは相似でLH：LB＝1：3。・・・㋑
㋐と㋑よりBI：IL：LH＝2：1：1となる。

（答え）　BI：IL：LH＝2：1：1

（2）
（1）の㋐と同様の考え方で、KD＝KGとなるのでIKとADは平行であり、三角形JGCと三角形JKIは合同で面積は等しくなる。
よって、四角形IJKLの面積＝三角形JCGの面積×2となる。

（1）の㋑と同様の考え方で、JG：JD＝1：3となるので、三角形JCGの面積×4＝三角形GDCの面積（＝四角形IJKLの面積×2）。
さらに、三角形GDCの面積×４＝平行四辺形ABCDの面積となる。

これらを１つの式にすると、
平行四辺形ABCDの面積＝三角形GDCの面積×４＝（四角形IJKLの面積×2）×4
よって、
平行四辺形ABCDの面積＝四角形IJKLの面積×8とわかる。
平行四辺形ABCDと四角形IJKLの面積の比は8：1。

（答え）　8：1

（3）
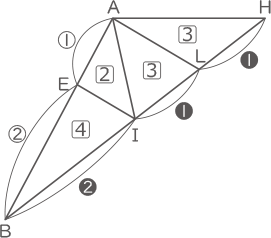
比より、
三角形AIEの面積：三角形BIEの面積＝1：2＝2⃣：4⃣
三角形IALの面積：三角形HALの面積＝1：1＝3⃣：3⃣
三角形BAIの面積：三角形HAIの面積＝1：1＝6⃣：6⃣