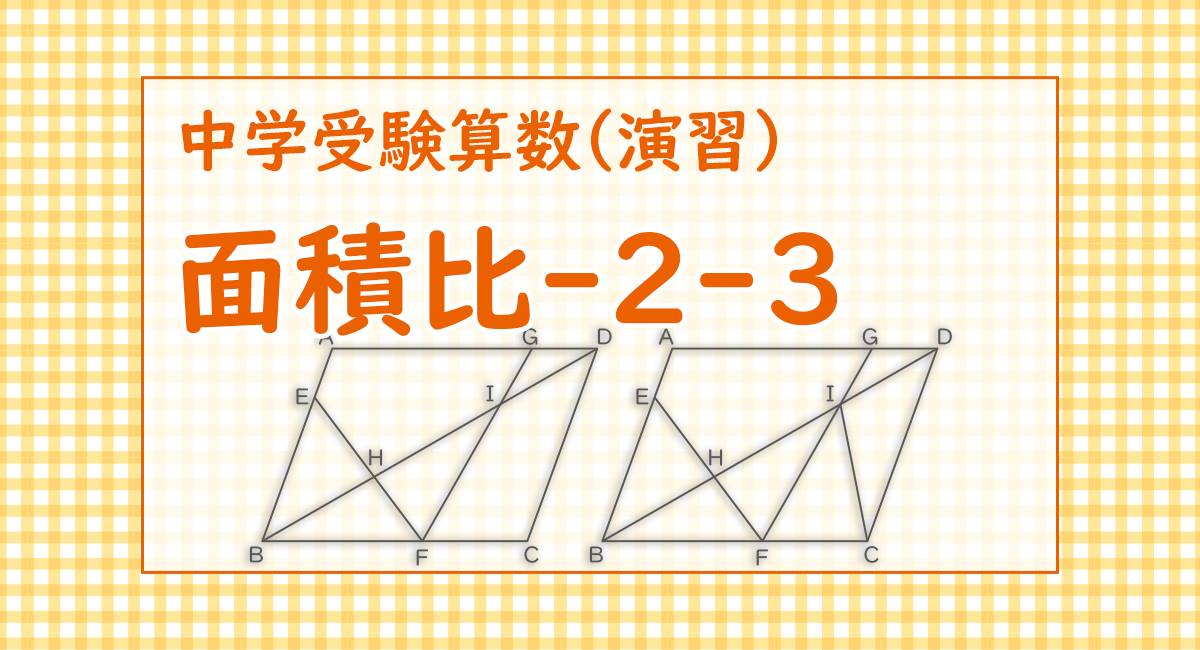
問題
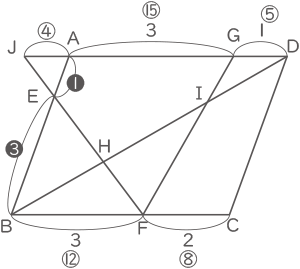
図の平行四辺形ABCDは,AE:EB=1:3,AG:GD=3:1,BF:FC=3:2です。
答えを出すために必要な式,図,考え方なども書きなさい。
(1) BH:HI:IDを,最も簡単な整数の比で表しなさい。
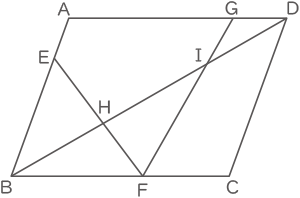
(2) 四角形HFCIの面積は平行四辺形ABCDの面積の何倍ですか。
教室には遠くて通えない、通塾負担を減らしたい。もしくは他の習い事が忙しくて、通塾の時間が取れない・・・ そんなご家庭に最適! 4大塾に通いながら弱点補強を家庭教師に任せているご家庭も多々、塾のクラスを上げるためにピンポイントでうまく利用しましょう。なにはともあれ資料請求してお子さんに合うか見てみましょう。
解答
- 解答を開く
-
図の平行四辺形ABCDは,AE:EB=1:3,AG:GD=3:1,BF:FC=3:2です。
答えを出すために必要な式,図,考え方なども書きなさい。(1) BH:HI:IDを,最も簡単な整数の比で表しなさい。

(2) 四角形HFCIの面積は平行四辺形ABCDの面積の何倍ですか。

(1)
ADとCBは同じ長さなので、AG:GD=3:1とBF:FC=3:2を4と5の最小公倍数⑳を全体の長さとして表すとAG:GD=⑮:⑤とBF:FC=⑫:⑧となる。
EFとADの延長線上の交点をJとすると、三角形EBFと三角形EAJは相似となり、
EB:BF=EA:AJとなるので、❸:⑫=❶:AJより、AJ=④となる。
三角形HDJと三角形HFBは相似なので、BF:DJ=HB:HD=⑫:㉔=1:2
三角形IBFと三角形IDGは相似なので、BF:DG=IB:ID=⑫:⑤=12:5
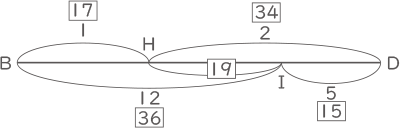
HB:HD=1:2とIB:ID=12:5を、3と17の最小公倍数$ \fbox{51} $を全体の長さとして表すと、HB:HD=$ \fbox{17} $:$ \fbox{34} $とIB:ID=$ \fbox{36} $:$ \fbox{15} $となり、HIは$ \fbox{19} $となる。
(答え) 17:19:15
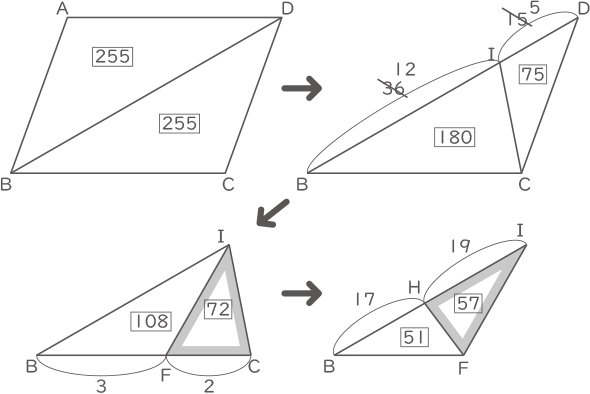
(2)
BH:HI:ID=17:19:15の比の数の和51と、BF:FC=3:2の比の数の和5の最小公倍数$ \fbox{255} $を三角形BCDの面積とする。
($ \fbox{255} $を使うのは、面積比の計算の際にBDを三角形の底辺と考える場合とBCを三角形の底辺と考える場合があるので、計算を楽にするため。)
平行四辺形の面積は$ \fbox{255} $×2=$ \fbox{510} $
四角形HFCIの面積は$ \fbox{72} $+$ \fbox{57} $=$ \fbox{129} $
$ \displaystyle \frac{129}{510} $=$ \displaystyle \frac{43}{170} $(答え) $ \displaystyle \frac{43}{170} $倍