問題
次の各問いに答えなさい。
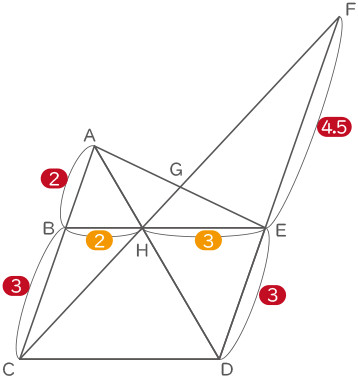
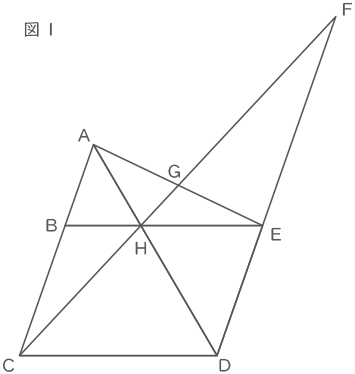
図1の四角形BCDEは平行四辺形で、AB:BC=2:3です。
(1) DE:EFを、もっともかんたんな整数の比で表しなさい。
(2) 三角形CDHの面積は、三角形EGHの面積の何倍ですか。
Amazonブランドのタブレット[Fire HD 10 Plus タブレット10.1インチ]フルHDディスプレイ(1920×1200)だから広くて見やすく家勉の必需品。
解答
- 解答を開く
-
次の各問いに答えなさい。
図1の四角形BCDEは平行四辺形で、AB:BC=2:3です。(1) DE:EFを、もっともかんたんな整数の比で表しなさい。
(2) 三角形CDHの面積は、三角形EGHの面積の何倍ですか。

解答までの道のりは複数あるが、今回は三角形AHEに着目して進む。
(ⅰ) 三角形AHEの面積:三角形CDHの面積を求める
(ⅱ) AG:EGの比から、三角形AGHの面積:三角形EGHの面積を求める。(1)
三角形ABHと三角形DEHは相似より、BH:EH=2:3。
三角形HBCと三角形HEFは相似より、BC:EF=3:4.5
よって、DE:EF=3:4.5=2:3
(答え) 2:3
(2)

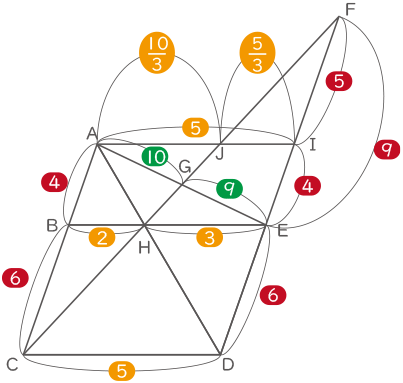
点Aを通り、CDに平行な直線を追加し、DFとの交点をI、CFとの交点をJとする。
(赤の比は2倍し、計算しやすい数字にしてある)
三角形FDCと三角形FIJは相似より、CD:DF=1:3=JI:IF=JI:5
JI=$ \displaystyle \frac{5}{3} $とわるので、AJ=5-$ \displaystyle \frac{5}{3} $=$ \displaystyle \frac{10}{3} $
三角形GAJと三角形GEHは相似より、AG:EG=$ \displaystyle \frac{10}{3} $:3=10:9三角形CDHと三角形CDBは同じ面積で、三角形HEAとHEIは同じ面積なので、三角形CDHの面積:三角形HEAの面積=5(オレンジ)×6(赤):3(オレンジ)×4(赤)=30:12=5:2。
三角形EGHと三角形AGHは同じ高さでAG:EG=10:9なので、面積比も10:9となる。
よって、三角形CDHの面積:三角形EGHの面積=5:(2×$ \displaystyle \frac{9}{19} $)=5:$ \displaystyle \frac{18}{19} $=95:18
95÷18=5$ \displaystyle \frac{5}{18} $倍(答え) 5$ \displaystyle \frac{5}{18} $倍