問題
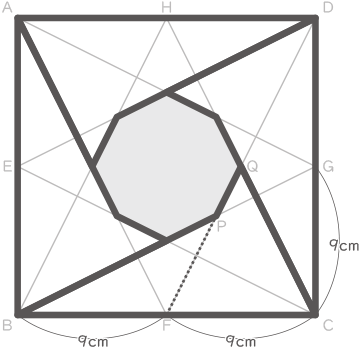
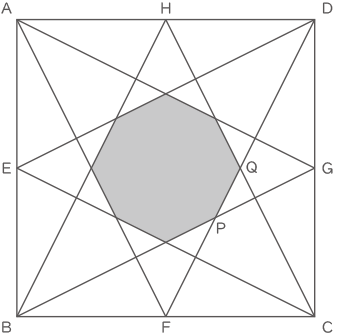
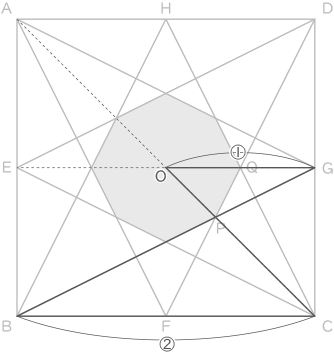
1辺の長さが18cmの正方形ABCDにおいて、各辺の真ん中の点E、F、G、Hと頂点を結んだ図です。また、BGとDF、CHとDFの交点をP、Qとします。
次の問いに答えなさい。
(1) BP:PGを、最も簡単な整数の比で表しなさい。
(2) △BFPの面積を式を書いて求めなさい。
(3) 図の色を付けた部分の面積を求めなさい。
灘をはじめ、名だたる難関中学に毎年多数の合格者を出す「浜学園」。講師の質や、教材のよさは折り紙付き。引きつりそうな料金設定ですが、中学受験をすると決めたら偏差値を買うんだ!ぐらいの前向きな気持ちで行きましょう。気になる方は資料請求してお子さんに合いそうか是非確認してみましょう。もちろん、体験入塾も無料で用意されています。
解答
- 解答を開く
-
1辺の長さが18cmの正方形ABCDにおいて、各辺の真ん中の点E、F、G、Hと頂点を結んだ図です。また、BGとDF、CHとDFの交点をP、Qとします。
次の問いに答えなさい。
(1) BP:PGを、最も簡単な整数の比で表しなさい。
(2) △BFPの面積を式を書いて求めなさい。
(3) 図の色を付けた部分の面積を求めなさい。 (1)
(1)
図形内に相似な三角形を作る。
OG:CB=2:1なので、BP:PG=2:1(答え) 2:1
(2)
三角形BFPの面積=9×9×$ \displaystyle \frac{2}{3} $×$ \displaystyle \frac{1}{2} $=27cm2(答え) 27cm2
(3)
図の様に、四角形BPQCと同形状の図形4つに分けられる。
問(2)より、三角形BFPの面積=27cm2
三角形FCQの面積=三角形FCGの面積=9×9×$ \displaystyle \frac{1}{2} $=$ \displaystyle \frac{81}{2} $図の色を付けた部分の面積=18×18-(27+$ \displaystyle \frac{81}{2} $)×4=54cm2

(答え) 54cm2

 (1)
(1)