問題
1辺の長さが12cmの正方形ABCDがあリます。
点E,F,G,Hはそれぞれ辺AB,BC,CD,DA上にあリます。また,点Pは正方形の内部にあリます。
以下の問いに答えなさい。
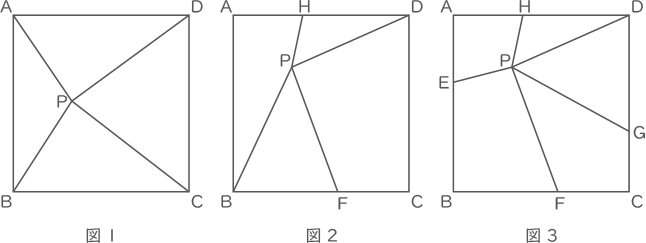
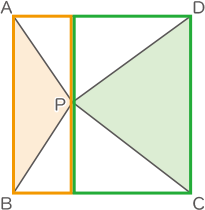
(1) 図1において,三角形PABと三角形PCDの面積の和は何cm2ですか。
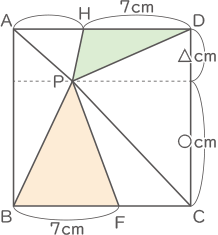
(2) 図2において,辺BFと辺DHの長さがどちらも7cmのとき,三角形PBFと三角形PDHの面積の和は何cm2ですか。
(3) 図3において,辺BFと辺DHの長さがどちらも7cm,辺AEと辺CGの長さがどちらも4cm,四角形AEPHの面積が18cm2のとき,四角形CGPFの面積は何cm2ですか。
教室には遠くて通えない、通塾負担を減らしたい。もしくは他の習い事が忙しくて、通塾の時間が取れない・・・ そんなご家庭に最適! 4大塾に通いながら弱点補強を家庭教師に任せているご家庭も多々、塾のクラスを上げるためにピンポイントでうまく利用しましょう。なにはともあれ資料請求してお子さんに合うか見てみましょう。
解答
- 解答を開く
-
1辺の長さが12cmの正方形ABCDがあリます。
点E,F,G,Hはそれぞれ辺AB,BC,CD,DA上にあリます。また,点Pは正方形の内部にあリます。
以下の問いに答えなさい。
(1) 図1において,三角形PABと三角形PCDの面積の和は何cm2ですか。
(2) 図2において,辺BFと辺DHの長さがどちらも7cmのとき,三角形PBFと三角形PDHの面積の和は何cm2ですか。
(3) 図3において,辺BFと辺DHの長さがどちらも7cm,辺AEと辺CGの長さがどちらも4cm,四角形AEPHの面積が18cm2のとき,四角形CGPFの面積は何cm2ですか。 (1)
(1)
Pを境に左右に長方形を作ると、オレンジ色の半分の面積がPAB、緑色の半分の面積がPCDとなる。
よって、求める面積は正方形ABCDの半分となり、
12×12÷2=72cm2(答え) 72cm2
 (2)
(2)
図の様に、Pより上の高さを△、下の高さを〇とすると、求める面積は、
7×△×$ \displaystyle \frac{1}{2} $+7×〇×$ \displaystyle \frac{1}{2} $=(△+〇)×$ \displaystyle \frac{7}{2} $
△+〇は12cmなので12×$ \displaystyle \frac{7}{2} $=42cm2(答え) 42cm2
(3)
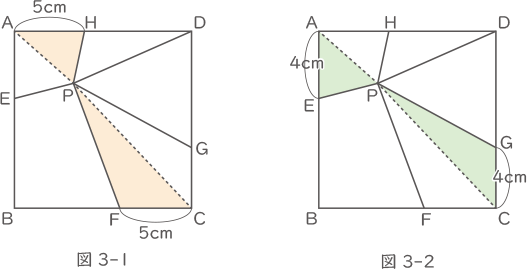
次の2つの図の様に補助線を引き、色の付いた部分の面積を(2)と同様に求める。
図3-1の色の付いた部分の面積は、
12×$ \displaystyle \frac{5}{2} $=30cm2
図3-2の色の付いた部分の面積は、
12×$ \displaystyle \frac{4}{2} $=24cm2合わせて30+24=54cm2
よって、四角形CGPFの面積は54-18=36cm2(答え) 36cm2

 (1)
(1) (2)
(2)